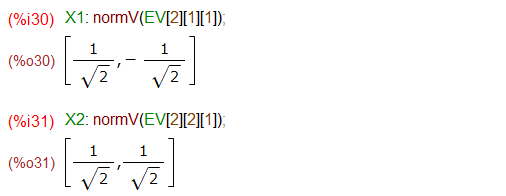今回は、処理の手順としては前々回の復習です。「対称行列を直交行列つかって対角化する」ってやつです。でも前回トートツにマクローリン展開などしていたので、既に前々回の手順は忘却の彼方へ。困ったもんだ。それにしても2次形式とかその標準形とか楕円とか、これまたトートツ感あるんですが。
※「忘却の微分方程式」投稿順 index はこちら
※以下の実習は、みんな大好き Maxima 様の以下のバージョン(Windows)で行なっております。
-
- wxMaxima 21.05.2
- Maxima 5.45.1 (wxMaximaの裏で動いているMaxima本体)
※以下の参考書の「改訂1」版の演習問題を題材に使わせていただいております。
昔、こういう御本があればも少し数学できるようになったのになあ。そこで今はMaxima様に丸投げするのであります。
上記の御本から今回テーマの真髄を1行引用させていただきます。
直交変換では、”大きさ” や “角” が保存されるので、図形の形はそのままに、座標系が変わったと考えればいいんだよ。
今回の問題
以下の2次曲線の左辺を標準形に直し、それが楕円であることを確認する
ここで、2次形式とその標準形は以下のようです。真ん中のXとY混ざっているやつが邪魔なので抹殺せよと。ホントか?
そのとき、2次形式は対称行列であるAをつかって以下のように書けるので
行列Aを対角化する直交行列Uを求め、Uの逆行列Wによって元の座標系 x,y を、新たな座標系 xN, yN に直交変換すれば標準形になるのだ、と。知らんけど。
まずは元の変換行列から
上記の%o25と%o24、そして問題の2次曲線の左辺を眺めれば、対称行列Aは以下のようになることが分かります。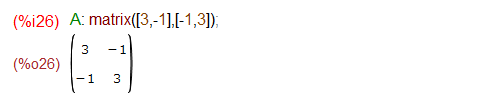
以下の回で必要な操作は既にやっております。手順はそのまま
忘却の微分方程式(52) 反復練習16、対称行列Aを直交行列Uを用いて対角化、Maxima
まずは、固有値、固有ベクトルを求めます。Maxima様お願い!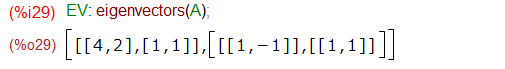
上記の結果から固有ベクトルを求めるためのちょいと準備(いつもの)をしておきます。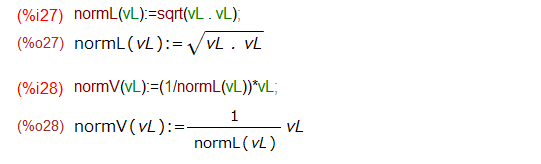
固有ベクトルを取り出します。
上記固有ベクトルをガチャンコして直交行列Uを求め、さらにAを対角化してみます。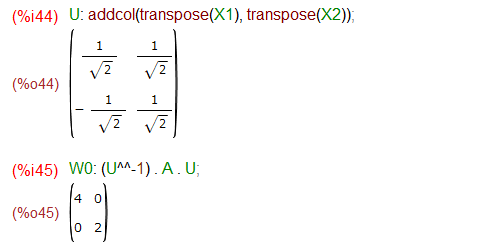
上記から、新たな座標系では左辺は以下のようにかけると知れます。ホントか?
おっとどっこい約分してなかったデス。ま、いいか。いい加減だな。いつものことよな。