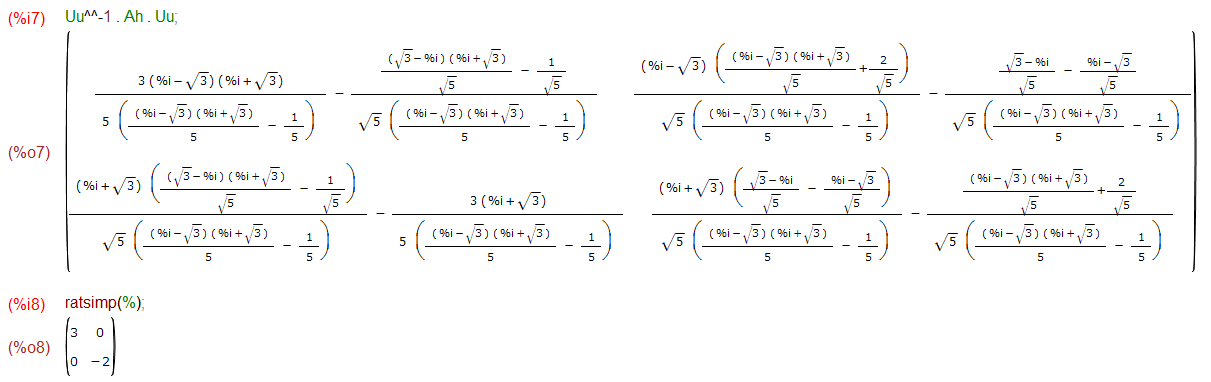今回から複素行列、複素ベクトルに入ります。電子デバイス的にはAC波形を扱うときに毎度複素数にお世話になっております。しかし、エルミートとか、ユニタリとか聞いても聞かなかったフリをしている年寄りです。でもね、Maxima様に置かれましては実数も複素数もないです。淡々と解いていただけます。お前は何をするのじゃ、と。
※「忘却の微分方程式」投稿順 index はこちら
※以下の実習は、みんな大好き Maxima の以下のバージョン(Windows)で行なっております。
-
- wxMaxima 21.05.2
- Maxima 5.45.1 (wxMaximaの裏で動いているMaxima本体)
※以下の参考書の「改訂1」版の演習問題を題材に使わせていただいております。(遥かな昔、こういう御本があったれば学校の試験もちっとは楽だったかもしれんです)
今はMaxima様に丸投げ、分かってなくても答えが出てしまうのであります。良いのかそんなことで。
conjugate() 関数
今回、おおいにお世話になる関数が conjugate です。conjugate(x)は xの複素共役な数を返す関数です。日本語マニュアルの掲載箇所が以下に。
エルミート行列
Maxima式?にエルミート行列を定義するならば、「conjugate()して, transpose()して元のAhと等しくなる」複素行列Ahがエルミート行列であります。以下にAhの例を。
conjugate(複素共役)をとり、transpose(転置)すれば元に戻ると。実行列であれば対称行列(複素共役は不要だけれど)であります。
ユニタリ行列
再びMaxima式?にユニタリ行列Uuを定義するならば、
transpose(conjugate(Uu)) . Uu = Uu . transpose(conjugate(Uu)) = E
であります。複素共役とって転置した行列と元の行列の行列積が等しく、かつ単位行列Eになる行列と。
これまた以下にUuの例を掲げますが、ratsimp()関数を忘れるとボロリンと計算途中の未整理な状態が表示されるのでビックリします。
エルミート行列Ahをユニタリ行列Uuを用いて対角化
上記例のエルミート行列Ahは、上記例のUuを用いて対角化できると。やり方は実行列とまったく同じ。
Uu-1 . Ah . Uu
実際に計算しているところが以下に(ratsimpを忘れてビックリし、慌ててratsimpかけている様子が冒頭のアイキャッチ画像に。)
つまりは、実行列のときに対称行列から変換行列を求めて対角化したようにエルミート行列からユニタリ行列を求めれば複素行列についても対角化できるのだ、と。さてその方法は基本同じだと。
エルミート行列からユニタリ行列を求める手順
単位ベクトルを求めるのにはベクトルの大きさを正規化しないとなりません。実ベクトルではx, y, …要素を二乗して加え合わせて開いて、割って、してました。本当は、複素ベクトルでやるように、複素共役なベクトルとの間の内積をとってから開いて、割ってする必要があります。当然、複素ベクトル用は実数用を包含してます。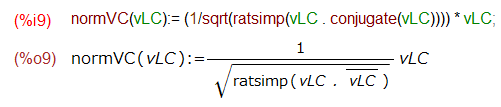
後は、過去の回で実数行列に繰り返し適用してきた方法と同様
-
- 固有ベクトルを求める(eigenvectors)
- 求めた固有ベクトルを単位ベクトルにそろえて変換行列(ユニタリ行列)に仕立てなおす
という手順であります。AhからUu(以下ではUxと表記)を求めてみたものが以下に。
上のUuと同じ値のUxになるように、正規化された固有ベクトルの一つX1を求める前に」固有ベクトルに値(%i+sqrt(3))をかけてます。何を乗じても固有ベクトルであることは変わらないので「都合がよくなる」値を掛けました。
なんだかな~。Maxima様があれば計算できそうだけれども、自分じゃゼッてー計算なんかできない。最初の1,2歩目で諦めるね、きっと。