前回、前々回と2回も微分を練習しました。微分は「機械的に」解けるし、もういいかとも思ったのです。しかし前回から今回の間に Maxima / wxMaxima 処理系を更新したので動作確認の意味を含めて(動かないわけないのだけれど)も少し微分をつづけたいと思います。微分というより、微分した後の「後始末」の練習ですかね。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。不埒な。
こういう御本がその昔にあったればよかったな。
パソコン更新、処理系も更新
ようやくWindows10パソコンをWindows11パソコンで更新いたしました。これにともない各種ソフトウエアも最新版をインストール中であります。今回はMaximaおよびそのWindows上のGUIフロントエンドであるwxMaximaです。インストールしたバージョンは以下です。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
wxMaximaのGUIの見た目も微妙に変化している感じがいたします。使用の最初にちょっと驚いたのが、
掛け算の記号として * (アスタリスク)キーをたたいたら、・表示された
という一件。コンピュータ言語で掛け算が * であるのは古代からの伝統ではありますが、数学的には美しくない、と。そこに手を入れていたのですな。でも*を書きたいときにはどうなるのかしら(後で調べます。)なお、Mathematicaでは変数をスペースでつなぐと掛け算になるスタイルで、あからさまな掛け算記号は現れないです。
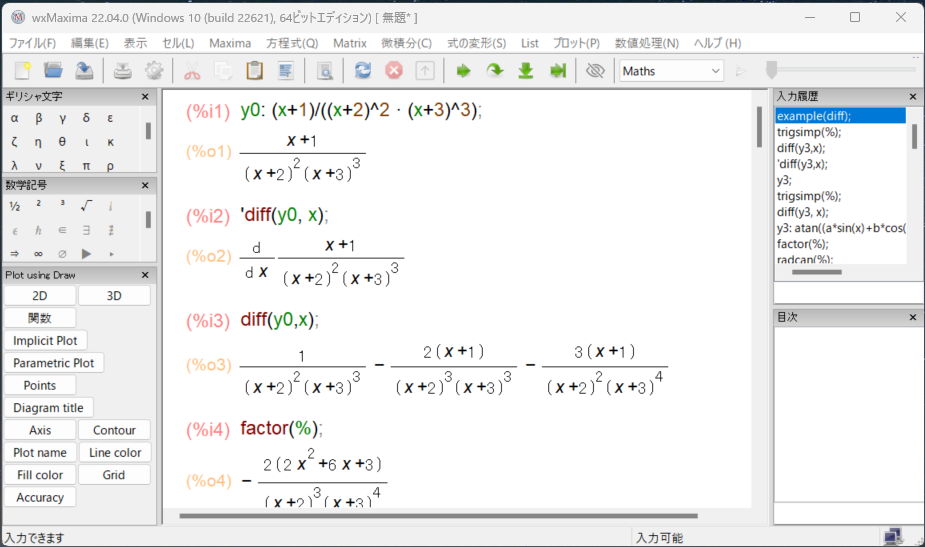
教科書じゃ「対数微分法」のページ
江川先生のご本では「対数微分法」として解法が解説されとりますがMaximaでは何も考えずにdiffに関数を渡すだけです。なお「対数微分法」は、f(x)^g(x)みたいな形式の場合に両辺の絶対値の自然対数をとってから微分する方法、といったらいいですかね。
早速、掛け算記号で*を書いたらドットになりました。黄色のところ。
微分直後は例によってあんまりな形式です。ここでは一発 factor() で整理できました。
続いて「対数微分法」らしいべき乗の上にべき乗が載ってという関数。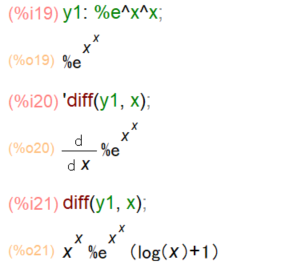
diff()一発で、整理の必要もありませなんだ。
逆三角関数はどうよ
プログラミング言語には、逆三角関数のお名前を arcsin のようにつづる系統と asinのようにつづる系統の2つがあるような気がしています。知らんけど。
この例題も単純微分適用後はアンマリな形です。そしてfactor()一発では綺麗にできなかったです。今回はまずradcan()で整理してから、最後factor()にお願いすると「いい感じ」になりました。
逆三角関数の中に三角関数がネストしている以下の場合はどうよ。
やっぱり微分直後はアンマリです。この場合三角関数がテンコ盛りなので、trigsimp()にお出まし願ってます。なんと、trigsimp()一発で綺麗に整理できてお答えは1。カタルシスを感じる(やっているのはMaxima様ですが)最終結果です。例題はこうでないと。