前々回、SPICEのマクロモデルの活用を「心に誓った」ものの、そのために越えなければならない山は沢山ある（ちんまい山だけれども）です。その最初の一つが「多項式による非線形な従属電源の表現」でないでしょか。POLY(1）などと書かれているヤツ。その後ろには数字がずらずらと並んでます。なんじゃこりゃ。
※「SPICEの小瓶」投稿順インデックスはこちら
ビヘイビアなマクロモデルと従属電源
実際の回路構成とは異なるけれど、ブラックボックスの外側から眺めればさもそれらしい動作をするビヘイビアなマクロモデルを構築するには、以下４つある「従属電源」を制覇することが必須なようです。
-
- Voltage Dependent Voltage Source … E/E2（電圧制御電圧源）
- Voltage Dependent Current Source … G/G2（電圧制御電圧源）
- Current Dependent Current Source … F（電流制御電流源）
- Current Dependent Voltage Source … H (電流制御電圧源）
どれも他のノード間の電圧とか電流とかに反応して、電圧なり電流を発生させるもの。一種の関数みたいなもの？ 従属電源を制するものがマクロモデルを制すると。誰が言ったそんなこと。
多項式近似
さて、例えば電圧制御電圧源の場合、どこか指定の制御ノード間の電圧に対して、単純にゲインを指定して、２倍の電圧を出力ノード間に発生しろ、みたいな指定ができます。これはゲインの数字１個を指定するだけなので簡単。しかし、強力なのは、POLYというキーワードにつなげて式を記述できることです。POLY＝多項式です。LTspiceのHELPから１行引用させていただくとそのSYNTAXはこんな感じ。
ううむ、何が何やらわからないっと。
-
- (node1+, node1-) などと書かれているのが制御ノードの組。この場合、node1+, とnode1-間の電位（仮にV1とします）が第１の制御電圧。
- 以降(nodeN+, nodeN-)までありますが、これがPOLY<N>のNと対応してます。N個の制御電圧があるという意味。N次元などと言われるかもしれません。
- これに続く c0 c1 c2 c3 c4 … は多項式の係数
N個の制御電圧に対する式を具体的に書くのはとても辛そうだったので、とりあえずPOLY(2)の制御電圧が２つだけのときを書いてみます。Vx、Vyのところは実際には２個のノード番号ペアに置き換わります。
POLY(2) Vx Vy c0 c1 c2 c3 c4 c5 c6 ...
そのときの従属電源の電圧は（^をべき乗演算子として使ってます。すみません。）
V = c0 + c1*Vx + c2*Vy + c3*Vx^2 + c4*Vx*Vy + c5 * Vy^2 + c6 * Vx^3 + ...
変数２個でもエライ話ですな。それに、… のところをいくらでも継ぎ足せる？し。知らんけど。
一番単純な１変数 POLY(1)の場合の記述が以下に。
POLY(1) Vx c0 c1 c2 ...
そのときの電圧は、こんな感じ
V = c0 + c1*Vx + c2*Vx^2 + ...
面倒だけれど、素子の特性を「多項式近似」した式があれば（表計算ソフトでも計算してくれるし）、それを真似する特性は自由自在だと。
制御ノード（変数）１、２次式の「デバイス」を作成してみた
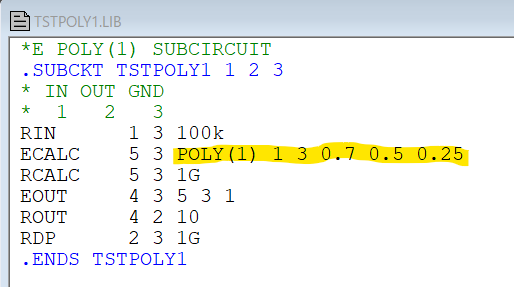
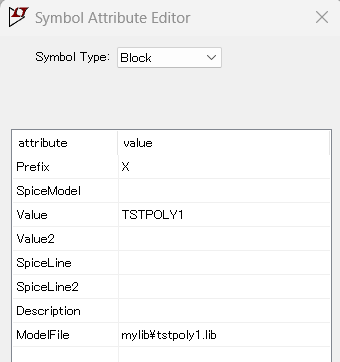
さっそく、LTspiceでシンボルを作ってみました。INとCOM間に印加された電圧の２次式で表される出力がOUTとCOM間に現れる「デバイス」のマクロモデルのつもりです。
上記の図よりも肝心なシンボルのアトリビュートがこちら。
プリフィックスはXなので、内部にはサブサーキットがやってくることになります。サブサーキット名はTSTPOLY1とな。そしてそのモデルファイルは上記のmylibフォルダにありと。
mylibフォルダに配置したサブサーキットが以下に。
早速、POLY使ってみました。黄色のマーカ部分。まず 1 3 とあるのは、ノード１と３の間の電位。つまりIN端子とCOM端子の間にあるRINという入力抵抗の両端の電圧っす。そこに現れる電圧をVとすると
0.7 + 0.5*V + 0.25*V2
という電圧をECALCという従属電圧源がノード 5 3 間に出力します。出力抵抗などの素子が間に含まれとりますが、ほぼそのままの上記２次式で表される電圧がOUT端子とCOM端子間に現れる筈。
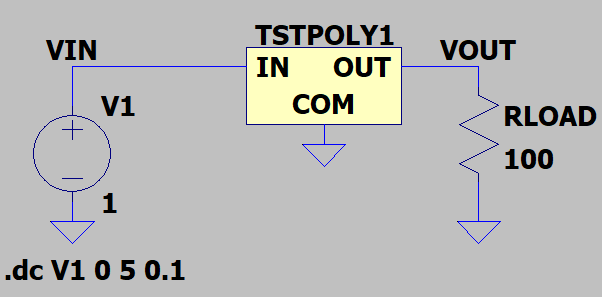
この「デバイス」をテストするための回路図が以下に。
上記設定にてDC解析をかけてみるとこんな感じ。
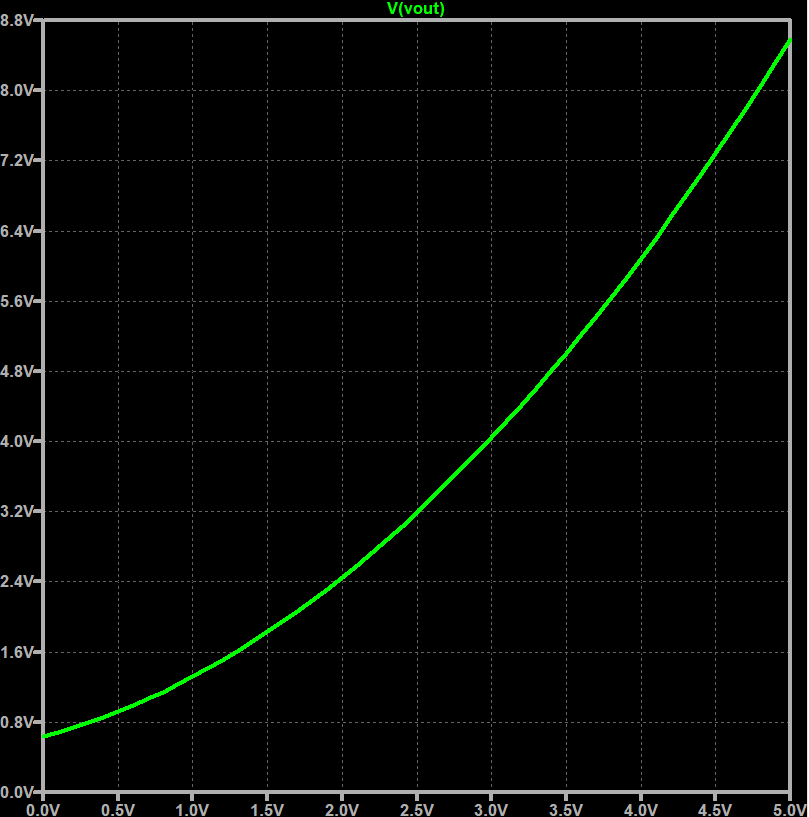
入力した２次式の雰囲気は出てるんでないかい。出力抵抗がチョッチ邪魔だけど。