前回、前々回と電圧制御電圧源のPOLY記法を使ってアナログ電圧の加減算、乗算のビヘイビアモデルを作ってLTspice上で動作確認。今回はアナログ電圧除算回路のビヘイビアモデルです。この除算の算法は自分ではとても思いつかなかったので、ほぼ30年前の例の御本を取り出してきてのぞき見。やっぱ数学できるヒトは違うよ。
※「SPICEの小瓶」投稿順インデックスはこちら
※ Analog Devices, Inc. LTspice XVII(x64) (17.0.36.0)を使用させていただいて動作確認しております。
POLY記法で割り算もできる?
カンニングに使ったご本の別シリーズ記事が以下に。
L.W.R.(44) 古文書編#14、SPICEによる回路設計(ディスク付)、1994年
SPICEのマクロモデル構築のために丸ごと1冊ささげられたご本です。これ見りゃマクロモデルなど簡単かというと、そうでもないのは書いてあることが難しいデス。特に数学苦手な年寄には。今回もどうやって割り算するのか理解するのに手間取りました。数学苦手な老人の読み解きをたどると以下です。
-
- 今回は電圧制御電圧源ではなく、電圧制御電流源を使う
- 2本の入力端子の電圧をVA、VBとする
- 2個の電圧制御電流源(電流IA, IB)と1個の抵抗(R)を並列に接続する。ただし、2個の電圧制御電流源の方向は逆とする
- このときRの両端の電位差をVXとする
- IAの方は入力電圧VAに対して比例定数Cで電流を制御、IA=C*VA
- IBの方は入力電圧VBおよびVXに対して比例定数Dで電流を制御、IB=D*VB*VX
- 電流の方向が逆なので、VX = R*(IA – IB)とかける
- IA、IBをVA、VBで書き直せば、VX = R*(C*VA – D*VB*VX)
- 両辺に現れたVXをまとめれば、VX = R*C*VA / (1+R*D*VB)
- ここでRを非常に大きい値(以下極限では無限大だが実際には1GΩとか)にもっていくと(なお以下の極限の計算は別シリーズでこれまたお世話になっておりますMaxima様)

上記のように C*VA/D*VB という割り算の関係になる。電圧制御のC、Dは単なる比例定数なので1,1とかに決めれば単純除算じゃと。
ここでPOLY記法を使えば、2つの電圧X, Yの乗算 X*Y が計算できる、というのがミソなんであります。
モデルファイル(.SUBCKT)
割り算モデルのモデルファイルが以下に。Gで始まるのが電圧制御電流源です。
SPICE記述すると簡潔。上記の説明を理解しなかったらなんでこれが割り算になるのか分かりません。お手上げだあ。
シンボル
上記のビヘイビアモデルをLTspiceの回路図上に配置するためのシンボルの定義が以下に。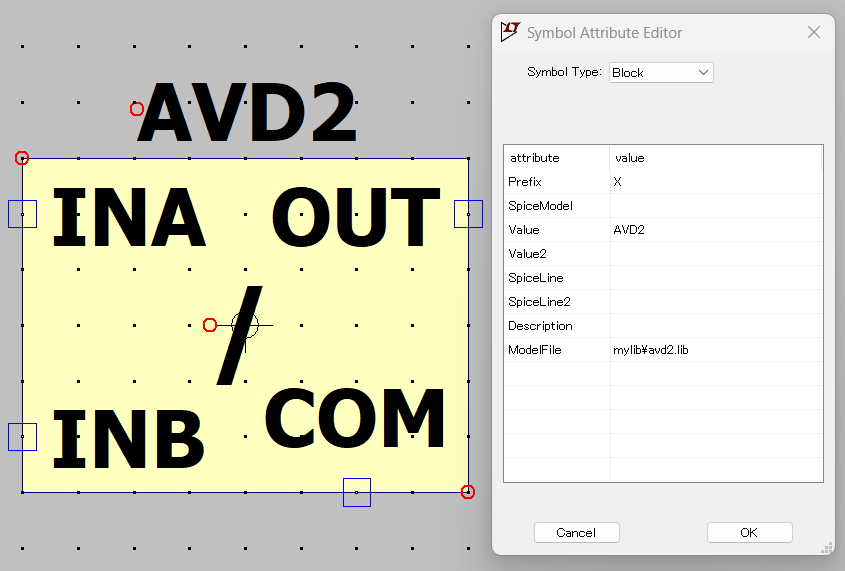
モデルをエクササイズするための回路
動作確認用の回路が以下に。ぶっちゃけ前回の掛け算モデル用の回路図のシンボルを入れ替えただけ。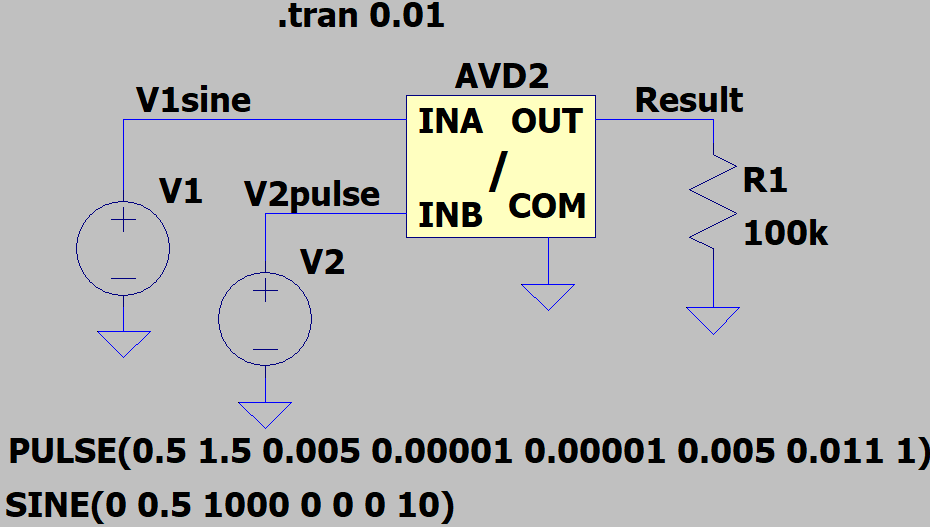
なお、入出力抵抗値はパラメータ化したので、忘れずに値を書き込んでおく。こんな感じ。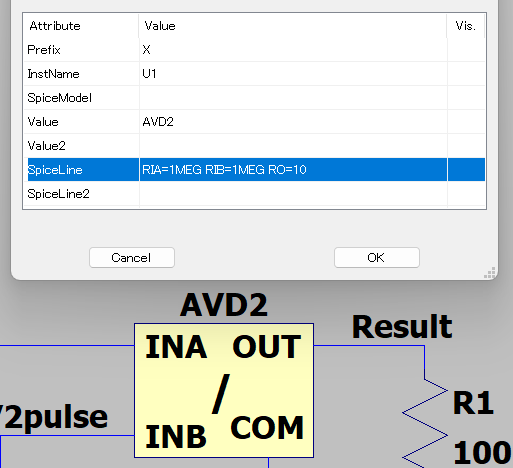
シミュレーション結果
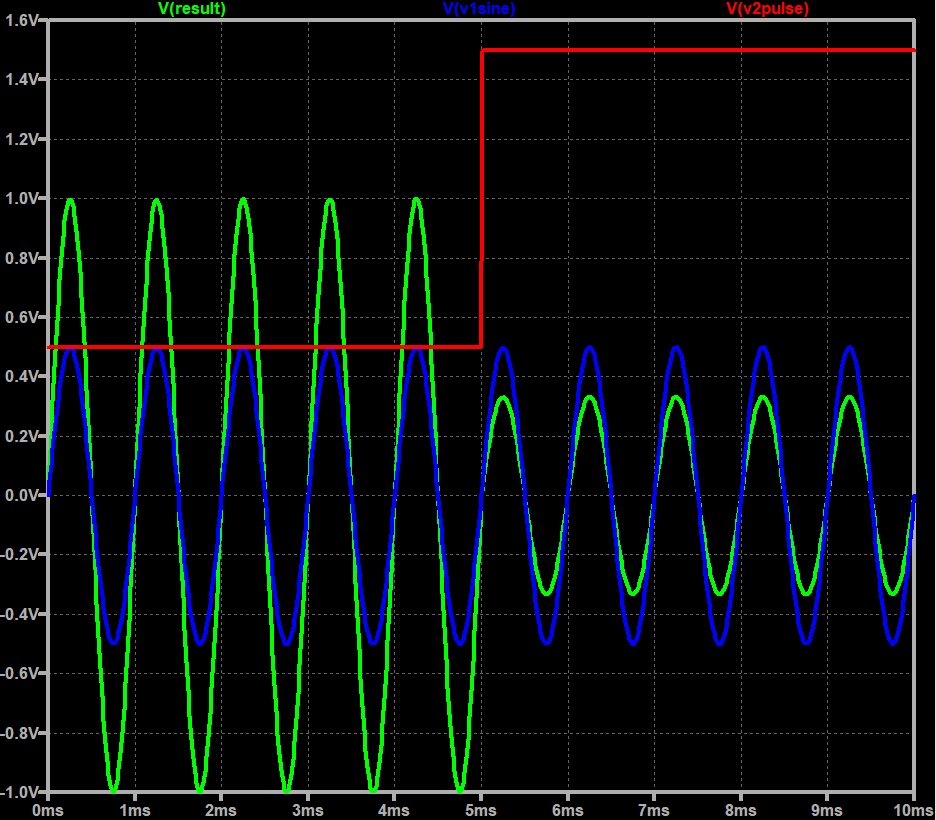
ちょっと見ずらい青色が被除数側の信号です。振幅0.5Vの正弦波。赤色が除数側のステップ的な信号。最初0.5Vで1.5Vに跳ね上がるもの。そして青を赤で割った結果が黄緑っす。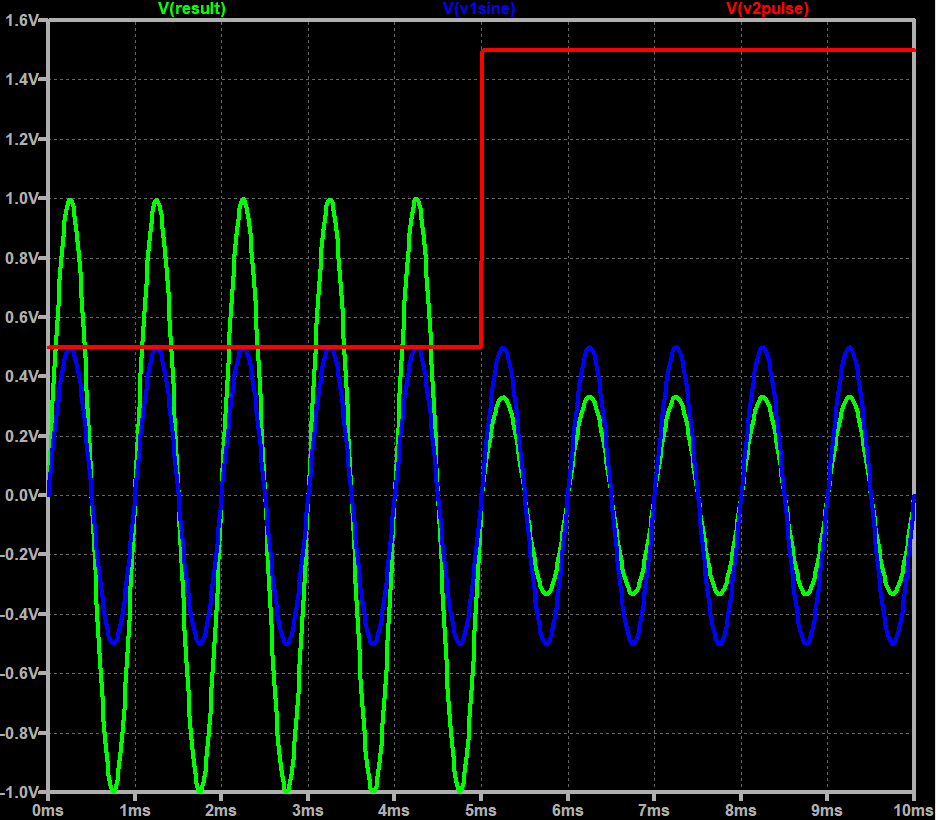
0.5で割ったら振幅は倍、1.5で割ったら振幅は3分の2だと。割り算も出来た?肝心のところちょろまかしだが。