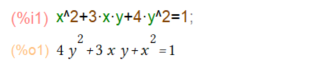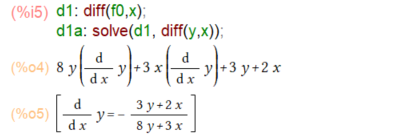大分前に「陰関数の微分」やってます。今回は「陰関数の２次導関数を求めよ（２階微分）」です。教科書的には偏微分を「駆使して」求める方針ですが、Maxima様にお願いするときは偏微分だろうが何だろうがdiff()一発です。でも例によってその後がメンドイ、陰関数はメンドイ。計算してもらってるのだから文句言うなよ、自分。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
陰関数の２次導関数
以下の回で「陰関数の微分」を練習してます。方法としては以下同文で２階微分も可能です。
忘却の微分方程式(65) 反復練習28、陰関数の微分、Maxima
まず例題の「陰関数」を以下に引用いたします。
ここの 4y2+3xy+x2=1 後で必要になるので覚えておきます。なんのこっちゃ。
さて、処理しやすいように上の式を左辺＝０の形に整理して f0 として保持しておきます。また、yはxに依存している陰関数であることを示すため、depends()しておきます。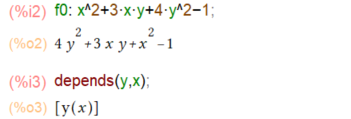
準備にひと手間かけても、陰関数の微分はdiff()一発とはいきませぬ。diff()の結果をみると以下のように(dy/dx)が式の中に現れてくる形です。所望のdy/dx=の形で求めるにはdiff()の結果をsolve()に渡してやらねばなりません。
まあ、これで１階微分はできたと。
２階の微分も、diff()の第３引数に２を指定すれば同様にでき、同様にsolveすれば変形もできるのですが、まだいけません。こんな感じ。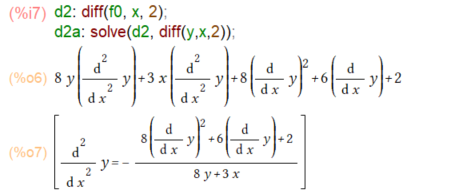
右辺の中に、dy/dxが現れています。こいつらを消して～。
カッコいい「消し方」が分からなかったので、力業でsubstしてしまいます。すでに１階微分の結果はx,yの式としてもとまっているので以下で行けます。それにしてもrhs(d1a[1])とかぱっと見わけわからんです。上の%o5のところをみたら分かりますが「１要素のリストd1aの第１要素の式の右辺」です。
substの後、現れいでたメンドクセー式をratsimp()かけてfactor()かけてそこそこな形にまで変形してみました。
そこで、以下f0=0であったことを思い出しますです。
つまり分子の（）の中は１なので、上の黄色のマーカ部分がお答えになると。今回も無理やり感が強いな。