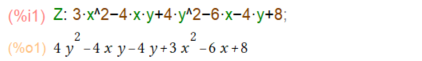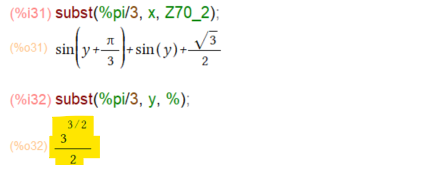忘却の微分方程式(96) 反復練習59、2変数関数の極値、三角方程式無理やり感、Maxima

Joseph Halfmoon

今回は２変数関数の極値です。当然偏微分とって調べるもの。最初の例題は型どおりにOK。楽勝とおもったら、次の三角関数の問題、偏微分は簡単（Maxima様おまかせ）だけれど三角方程式で躓きました。仕方がないので無理やり感満載で三角方程式の解を求めてお茶を濁しました。どうしたらよいのか？

※「忘却の微分方程式」投稿順 index はこちら

※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。

遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。

※以下のMaxima/wxMaximaバージョンで実習させていただいております。

２変数関数 f(x, y) が偏微分可能なとき、f(x, y)が(x0, y0)において極値をとるための必要条件は以下だそうです。

１次の偏導関数が0にならないといけないのね。この辺は１次関数と同じよな。しかし必要条件でしかないので、(x0, y0)は極値とは限らないっと。極値をあたえる候補でしかないデス。これを停留点と称するのだそうな。

さて、さらに(x0, y0)の近傍で２次偏導関数をもちいて

のとき

- Δ<0, A>0　ならばf(x0, y0)は極小値
- Δ<0, A<0　ならばf(x0, y0)は極大値
- Δ>0 ならば極値でない
- Δ=0 ならばΔでは判定不能

であると。判定不能ってのが不気味、あまりそばに寄りたくないです。

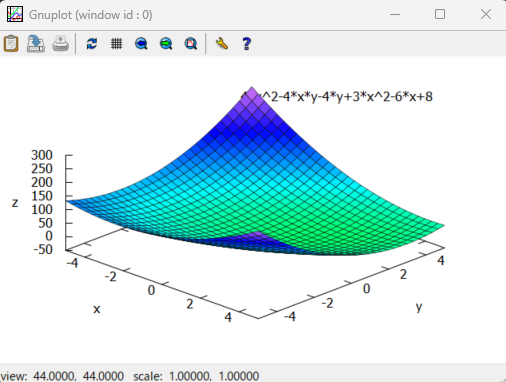
さて、最初の問題の２変数関数が以下に。

wxplot3d使えば３Ｄプロットできます。プロット見れば極値をとりそうなのか極小なのか、極大なのかの雰囲気はでてます。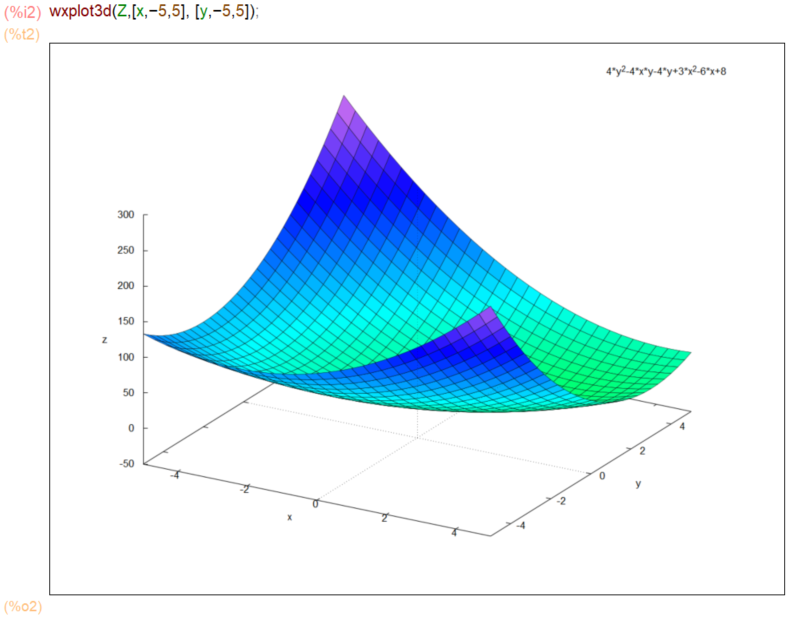

ただね、今回みたいなケースでは、いろいろ視点を変えて「極値に迫りたい」気がしてならないので、視点が固定されてしまうwxplot3dよりは、素のGnuplotを呼び出していただける plot3dコマンドを使った方が良い感じです。ポリゴンぐりぐりってやつ。

操作してみると、極小値がありそうな雰囲気。

さて、手順に従いまずは１次の偏導関数を求め、偏導関数が０になるような点（停留点）を求めてみます。こんな感じ。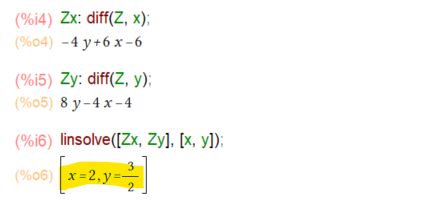

この問題は線形な連立方程式なので、シンプルにlinsolveで解けてよかった。

さて、２次の偏導関数を型通りにもとめてΔを使って判定してみます。２次になると皆数値になってしまって上記のx, yの値を代入する必要すらなくて、お楽。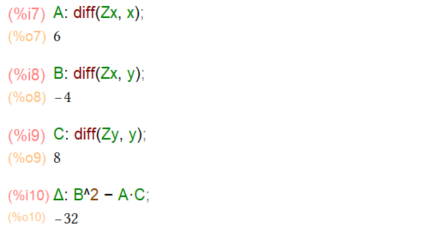

Δ＜０で、A＞０なので、極小値があると。まあ、当方グラフをみて予想していたとおり。その場所は、上の方で黄色いマーカ引いてある x=2、y=3/2という点なので、Zにその値を代入してみます。

極小値は -1 とな。

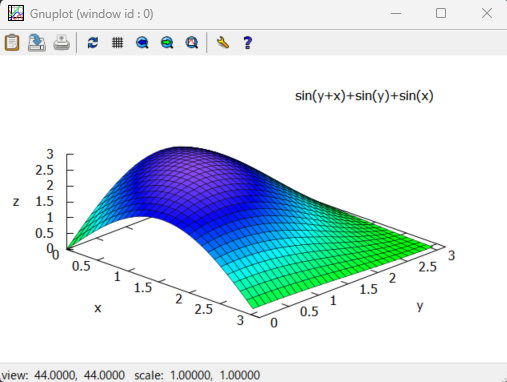
最初の問題が波乱なく完了したので、２つ目は三角関数使った問題をやってみます。しかしこれが意外と難物。まずは２変数関数が以下に。なお今回はx, yに条件あり、0<x<π、0<y<π です。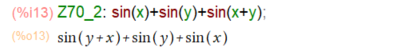

Gnuplotした結果が以下に。こんもりとした丘が見えます。多分、ほぼ確実に極大値がありそうですな。

さて手順通りにまず１次偏導関数。

三角関数なのでお答えも三角関数だよね。ここで

なる連立三角方程式を解いて x、yを求めれば停留点が求まる筈ですが、Maxima様に三角方程式を解いていただく方法が良く分かりませぬ。困りました。無理やり感満載で解いたのが以下に。

結局cos(y)=Yとおいて、Y=1/2とY=-1を求めましたが、条件 0<y<πによりY=-1は無し。cos(π/3)=1/2 であることから、x = y = π/3 です。こういう計算は高校生はお得意そうだが、年寄にはMaxima様のアシストあってもキツイっす。

さて手順通りに判定。substするたびに無理やり感があるなあ。

上記にようにΔ＝-9/4と負の値なので、極値が存在。またAはx=y=π/3の点で負なので極大値。

極大値を求めると以下のごとし。

求まることは求まったけれど、手で無理やり解いている感がありあり。どうしたものか。