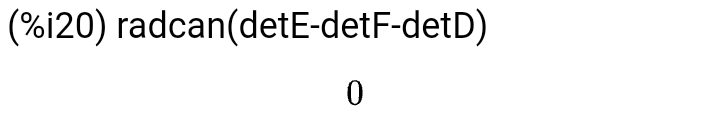前回に続き今回もスマホ上で動作するMaxima on Androidを使わせていただいて練習したいと思います。題材は行列式です。Maxima様相手にサラスの公式範囲にサイズを制限する理由は何もないのですが、入力がメンドイのと手計算用の例題を下敷きにしているので、今回はサラス公式で手計算できる3次範囲です。
※「忘却の微分方程式」投稿順 index はこちら
下敷きに使わせている参考書
本来は、数学の勉強のための以下の参考書(以下URLは「改訂9」)の「改訂1」版の演習問題をMaximaの練習用に使わせていただいております。
とても良い参考書じゃないかと思います。昔大学に入学したころに、こういう良い御本があったらと思う老人であります。
今回練習のソースコード
動かしてみると結構分量多く感じるのですが、ソースとしては以下の僅かな分量です。行列を定義して、行列式を求め、行列式の性質的な部分を順次確かめてみるもの。PC上のMaximaでもスマホ上のMaximaでも同じです。
A: matrix([1,2],[4, -1]); detA: determinant(A); B: matrix([2, 1, -1], [1, 3, 1],[2, -1, 1]); detB: determinant(B); C: matrix([2, 1, -1],[1, 3,1],[2,1,-1]); detC: determinant(C); C2: matrix([a, b, c],[a, b, c],[d,e,f]); detC2: determinant(C2); radcan(detC2); D:matrix([a,b,c],[d,e,f],[g,h,i]); DT:transpose(D); detD: determinant(D); detDT: determinant(DT); radcan(detD - detDT); E:matrix([a,b,c],[d+s,e+t,f+u],[g,h,i]); detE: determinant(E); F:matrix([a,b,c],[s,t,u],[g,h,i]); detF: determinant(F); radcan(detE-detF-detD); G:matrix([a, b, c],[x*d, x*e, x*f],[g,h,i]); detG: determinant(G); radcan(detG - x*detD);
MoA(Maxima on Android)上で実行
最初は数字の詰まった2次の行列Aの行列式 detA を求めます。
お次はやはり数字の詰まった3次の行列Bの行列式 detB。サラス公式のやつ。
次は、行列式の性質が現れているヤツ。数字が詰まった行列Cですが、1行目と3行目が同じ。このとき行列式は0になる筈。
同じことを、数字の詰まった行列でなく、文字で書かれた行列C2でやってみます。1行目と2行目が同じなので行列式は0になる筈。でもdeterminant()関数で行列式を求めただけでは文字式のままです。この結果を radcan()に渡して計算して整理してもらうと0になりました。良かった。
さて、次は転置行列の行列式の性質的なやつ。Dは3x3の文字で書かれた行列であります。DTはその転置行列です。transpose()関数で転置してます。それぞれの行列式を求め、結果2つを引き算してradcan()に渡せば0と。転置しても行列式は変わらんと。
お次は、先ほどの行列Dと、行列Dの2行目の各要素にs, t, uなんてものを足した行列Eと、行列Dの2行目をs, t, uで置き換えた行列Fについて
detE = detF + detD
などという関係が成り立つ、という話。
ここまでで行列式 detE, detF, detDが計算できているので、例によって引き算してradcan()にお願いすれば0だと。関係なりたっておりますな。
次は掛け算の性質、行列Dの2行目の要素にxをかけた行列Gの行列式detGと行列Dの行列式detDの関係
detG=x*detD
例によって淡々と計算し、最後radcan()にお願いすれば0だ、と。
こうしてスマホで計算出来てしまうのはありがたい限り。ホンダ様ありがとうございます。これ無しには計算不能な年寄り。