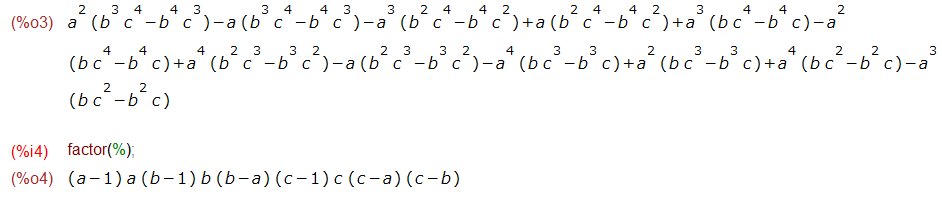最近、調子に乗ってスマホ上で言語処理系を動かしているためかスマホの電池の減りが速いです。そこでMaxima様についてはスマホ上のMaxima on Androidから、パソコン(WindowsPC)上のMaxima 21.05.2 利用に戻しました。Maxima様は特にPCだからとかスマホだからとか気にする必要もなし。
※「忘却の微分方程式」投稿順 index はこちら
※数学の勉強のための以下の参考書(以下URLは「改訂9」)の「改訂1」版の演習問題をMaximaの練習用に使わせていただいております。
昔線形代数をちゃんと勉強しなかったので反省を込めてお勉強しようと思ったのですが寄る年波には勝てず。計算辛いので、結局Maxima様のお勉強?になってしまっています。お願いすれば答えは出る、と。でもちょっと虚しい?
今回練習のソースコード
前回は、鉄板、サラスの公式範囲での行列式でした。行列式の性質的なところをちと触ってみた、と。今回はサラスの公式範囲を超える、といっても4次ですが、の行列式の計算です。
上記の参考書では余因子展開とか、よゐこはちゃんと覚えてね的な方法を駆使して3次以下に落として計算しているのであります。しかしMaxima様にお願いするときは、行列定義して determinant()関数に渡すだけっと。
今回使用のソースはわずかこれだけ。
X: matrix([1,1,1,1],[a,a^2,a^3,a^4],[b,b^2,b^3,b^4],[c,c^2,c^3,c^4]) detX: determinant(X); factor(%); Y: matrix([2,-2,4,2],[2,-1,6,3],[3,-2,12,12],[-1,3,-4,4]) detY: determinant(Y);
変数を含んだ第1の例題
第1の例題は、文字変数 a, b, c 入ってます。綺麗な行列ですが、とても自力で計算する気になれませんな(どうせ間違うケド。)行列式を求めるのに determinant()関数に行列を渡したら、案の定、a, b, c が沢山飛び出してきて目が回りそうです。
しかしね、Maxima様におかれましては、あわてず騒がずfactor()一発、因数分解すれば綺麗にお答えが求まります。
しかしなあ、因子の順番とか人間風味に並べ替える方法、ありそうなのだけれど難しそうで相変わらず手が出ません。
第2の例題、整数だけ
上記のようなケースが計算できるのですから、整数だけの4次の行列の行列式が計算できない筈がありません。
一撃。Maxima様も手持ち無沙汰な感じですが、行列式の章は通過したことにいたしとうございます。