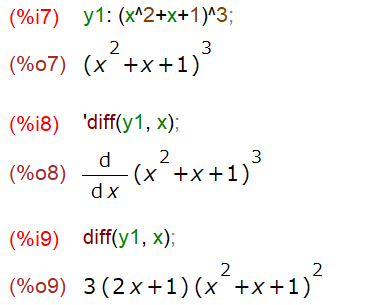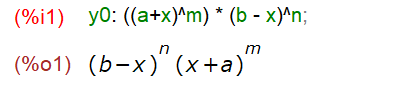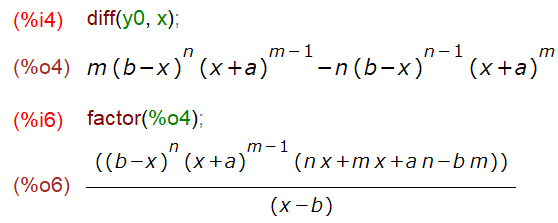今回から微分に入ります。微分こそ他力本願、ただただMaxima様におすがりすれば「機械的」に微分が出来ると。しかぁし!複雑な式でも難なく微分していただけるMaxima様ですが、微分した結果は、人間的に言うとチト汚かったりいたします。「所望の」形に持ち込むには何か別なお願いをせにゃならんと。
※「忘却の微分方程式」投稿順 index はこちら
不埒なことに以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
予備校の先生がお書きになっておられます。とっても分かり易いですが、数学の勉強には使ってないです。トホホ。
今回の手順
微分対象の関数をMaximaの関数 diff() に渡しさえすれば、微分をやってもらえます。しかし途中の「見栄え」もあるので、以下のようにしてみました。
まずは微分対象の関数を定義して、「その形」を観察。やっぱり%i1のような入力形式ではイマイチです。Maximaの出力形式の方が人間見やすいのではないかと。
一応、これから微分するぞ、という決意?を秘めて、「人間には分かり易い」形式を愛でます。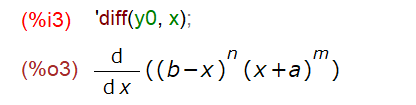
そのあと、シングルクォートを外して、微分を実施。ただ、その結果は複雑になり易いので、結果の変形(以下ではfactor)はまた別な話だ、と。
まずは一撃でできる奴ら
以下は、結果の変形などをしてみる必要のない、OKなケースかと。
つづいて、平方根が入ってきたですが、これまた結果をいじる必要もなしかと。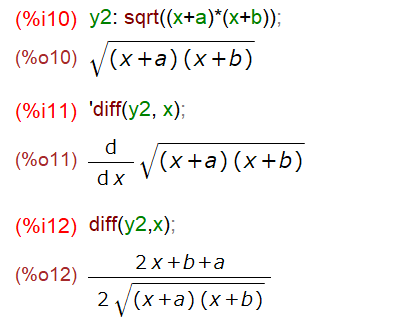
微分しただけではダメなやつ
以下の三角関数を含むやつも微分自体は簡単、でも結果がちょっと複雑すぎて何言っているのか分からないデス。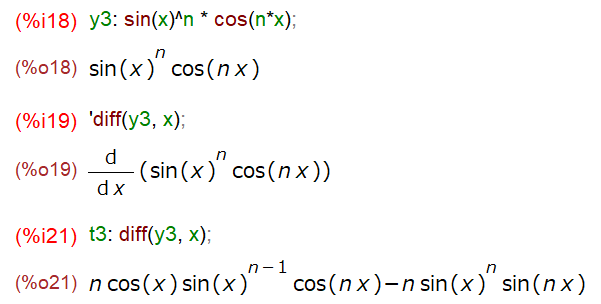
とりあえず 微分した結果に factor() かけてみました。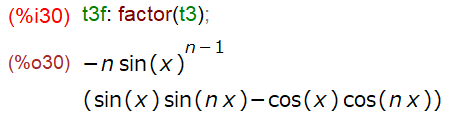
目立つのは、「sin sin – cos cos」 の部分(以下のところ)です。これって「加法定理」のあれ?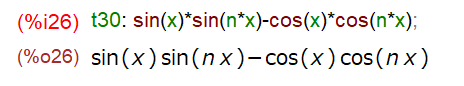
「sin sin – cos cosの形」に展開するときは trigexpand ですが、今回やりたいのは逆に「cos(A+B)」にする方なので trigreduce だと。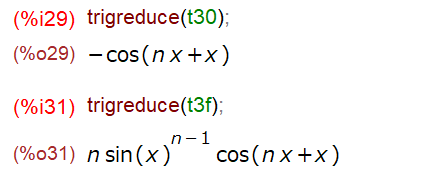
スッキリした微分結果になりました。微分するのは良いけれど、その後の変形を注文する方が難しい気がします。