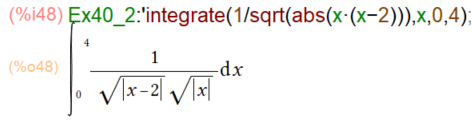積分区間の中に特異点のある異常積分(広義積分)など自分じゃ解ける気などしませんな。何言っているんだかわからない。しかし、他力本願 Maxima 様に御すがりすれば救っていただけると。衆生済度ってやつか?(ちょっと違うけど)でもま、準備だったり、後始末だったり、ちょっとは働かないとならないようです。知らんけど。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
区間の端に特異点があるケース
以下は積分区間 [0, a] の端、x=aが特異点であるような場合です。このような場合は、何も準備しなくても Maxima様は解いておしまいになるみたいです。前回同様、assumeはしてます。ちょろい?
積分区間の途中に特異点があるケース
しかし、以下のケースのように積分区間の中間点に特異点がある場合は、一撃とはいかない見たいです。
そこで苦し紛れに特異点(この場合はx=2)のところで積分区間を2つにわけて書き直してみたものが以下に。面倒なabs()を消してみました。そしたら定積分は一撃ですな。こんな感じ。
積分は出来たのですが、上のお答え(Ex40_2b)はイマイチ綺麗でないデス。数学の宿題的にはも少し整理しろや、といわれそう。
ついこの間、logの引き算を割り算に直す技(logcontract)を勉強したので、それ使って整理してみます。こんな感じ。
さらに、高校数学?的にはlogの中の分数を有理化するところまでやれよ、といわれそう。どうしたら簡単に有理化できるのか Maxima素人の老人にはわからなかったので、力技で以下のようにしてみました。
-
- まずlogの引数部分の分数のみを取り出す(Ex40_2d)
- 取り出したものをrat()関数に渡して有理化(そのときalgebraicというフラグをtrueにしておくのがミソみたいです。ホントか?)
- 有理化した結果をsubstで元の式の該当部分に戻してやる
なんだか、エレガントでないけれども、ま、一応それらしく変形はしてくれる(でも根号つかわずに指数で書かれてしまったけれど。)
欲張って多くは望みますまい。。。