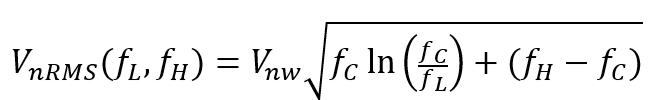前回は信号源インピーダンスで支配的なノイズ源が変わる件でした。そこでの議論の単位は入力換算ノイズnV／√Hzであり「スペクトル密度」だったです。雑音密度カーブを帯域で積分すればノイズの実効値(RMS)が求まります。しかし問題になるノイズは、ピーク・ツー・ピーク、たまに来るデカイやつ（尖頭値）が問題だと。確率的な存在？
※『OPアンプ大全を読む』投稿順indexはこちら
※「オペアンプ大全」はアナデバ様の以下のページからダウンロード可能です。
OPアンプ回路の基本から応用まで、OPアンプ大全を無償提供中
原著はOp Amp Applicationsという書物だったらしいです。
ノイズの実効値(RMS)
以下、ノイズの実効値を表す式を引用させていただきます。
周波数fLからfCまでが1/fノイズが支配的な周波数帯域です。そしてfCからfHまでがホワイトノイズが主な周波数帯域です。fCが1/fノイズのコーナ周波数であると。そしてVnwが前回学んだ雑音密度です。ルート記号の中の左側の自然対数を含む項が1/fノイズで、右側の引き算の項がホワイトノイズの項です。fCにくらべてfHが非常に大きければ、fCもfLも無視できてルートの中はfHだけとみなしても苦しゅうない、みたいっす。
ノイズの尖頭値(p-p)
上記の式でノイズの実効値(RMS)は計算できますが、実際にオシロスコープで観察できる時間波形に見えているのは尖頭値(p-p)です。実効値が決まればある尖頭値を超える時間割合を計算することはできるが、その絶対の上限などありはしないと。より大きな尖頭値が検出される確率は急速に減少するけれどもゼロではないのだと。
ちょっと蛇足ですが、地震学のグーテンベルグ・リヒター則ってやつとのアナロジーを感じましたぜ。マグニチュードがデカいやつほど頻度が減るやつ。知らんけど。ま、どちらも統計的（確率的）な存在。ホントか？
さて実効値RMSが求まれば、尖頭値[V]に対してその尖頭値を超える電圧が発生する「時間の割合」を求めることができるそうな。
-
- 尖頭値として２倍のVRMSをとると、なんとその割合は32%
- 尖頭値として４倍のVRMSをとると、割合は4.6%と急激に低下
もっとも一般的に使われる尖頭値の係数は6.6倍であるそうな。そのときの割合0.1%、つまりは99.9%は6.6倍以内におさまるってことね。それで6.6倍。ようやく謎のマジックナンバーの一つが分かった？