前回はビヘイビアモデルではなく実回路化可能と思われる（やってないケド）三角波‐正弦波変換回路（折れ線近似）をLTspiceしてみました。今回はビヘイビアに戻ってモデルを作ってみます。マクローリン展開の係数を電圧制御電圧源のPOLYの係数にぶっこむという方法なのですが、教科書はちょいと小技を使ってました。流石。
※「SPICEの小瓶」投稿順インデックスはこちら
※ Analog Devices, Inc. LTspice XVII(x64) (17.0.36.0)を使用させていただいて動作確認しております。
電圧制御電圧源のPOLY記法とマクローリン展開
電圧制御電圧源、Voltage Dependent Voltage Sourceは、マクローリン展開との相性が良い感じです。
Exxx n+ n- POLY(1) nc+ nc- c0 c1 c2 c3 c4 c5 c6 c7 ...
n+, n- は電位差を与える２つのノードであり、POLY(1) は以下の係数が１制御変数の多項式近似であることを示しています。次のnc+ nc- は制御する側のノード２つでこの間の電圧をVとすると、Vの0乗の係数がC0（定数）、Vの１乗の係数がC1、という形で記述ができます。適当な次数で打ち切れば計算はそこで止まります。
ここで、高校だか、大学だかで教わった筈のSIN関数のマクローリン展開を思い出せば以下のようです。偶数次数が消えるのね。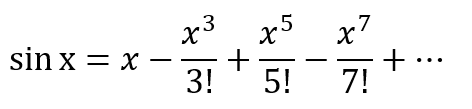
ここで出てくる 1/3!とかは簡単に計算できるので、それをそのままPOLYの係数にすればいいじゃん、と思うのですが、教科書をカンニングしたらば値が違いました。
入力三角波の振幅を -π/2 ~ π/2とすれば、そのままでもよいのですが、流石にSPICEシミュレーションで振幅π/2というのは抵抗があります。そこで振幅は１としておいて、そのπ/2倍の値を電圧として扱えば目的を達すると。ぶっちゃけ、係数の(π/2)**次数をあらかじめ含めておく、という小技です。
ビヘイビアモデルのソース
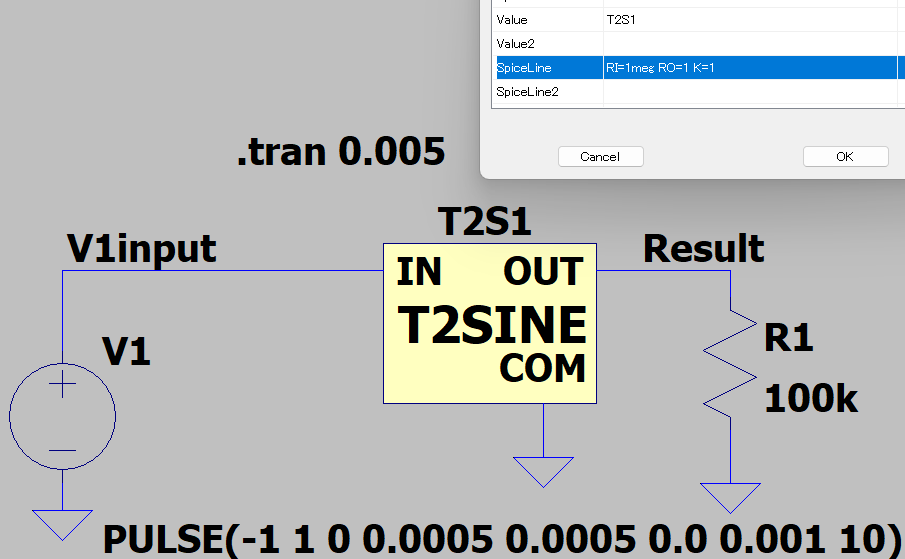
上記の小技を用いた三角波-正弦波変換（ただし三角波の振幅は１にしてね）のコードが以下に。一応、入出力の抵抗(RI、RO）と出力正弦波の振幅（入力１のK倍）はパラメータ化してあります。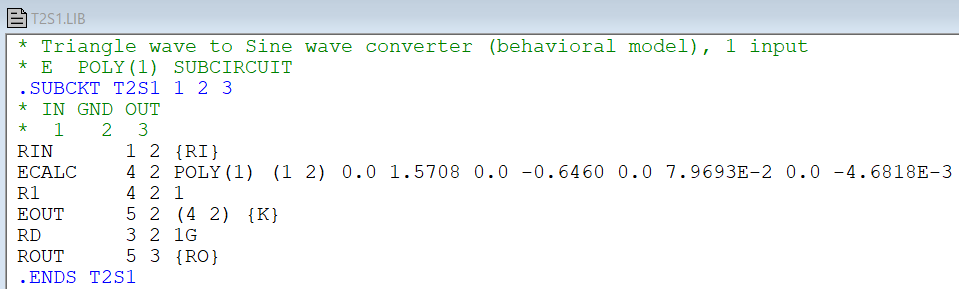
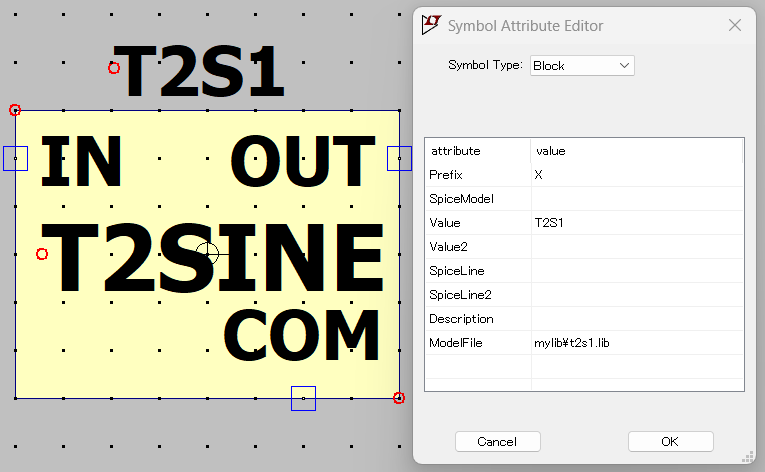
ビヘイビアモデルのシンボル
例によって四角で手抜きなシンボルが以下に。
動作確認用の回路
これまた手抜きな動作確認用の回路図が以下に。
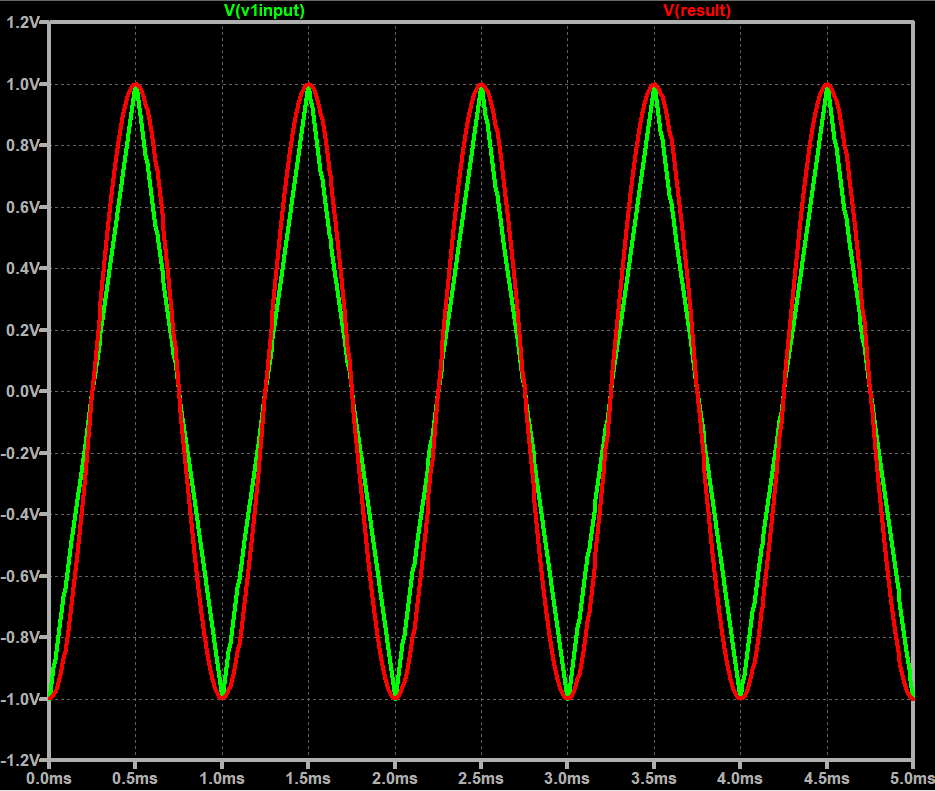
シミュレーション結果
黄緑色が振幅１、オフセット０の入力三角波です。赤色がゲインK＝１とした三角波-正弦波変換ビヘイビアモデルの出力です。
まあまあ、正弦波。近似とは言え７次の項までとってるもんね。