
このところBBC micro:bit v2のオンボードペリフェラルを端から見てまわっています。今回はオンボードというよりオンチップペリフェラルです。nRF52833搭載のハードウエア乱数発生器です。Goにはソフトウエアの乱数発生パッケージがありますが、多分ハードウエアで発生した方がより良いのではないかと。知らんけど。
※「GoにいればGoに従え」Go関連記事の総Index
nRF52833のRandom number generator
NORDIC Semiconductor社の以下の仕様書を参照させていただいとります。
nRF52833 Product Specification v1.5
上記には オンチップのペリフェラル回路の一つとして RNG – Random number generator があります。「モダーンな」マイコンでは素性のよいHWの乱数発生回路が最近必須になっているじゃないかと思います。上記を拝見するに「internal thermal noise」起源みたいなので、多分確実にジョンソン・ノイズでしょう。
ジョンソンノイズの公式を忘れてしまった「よゐこ」のためにノイズのRMSを与える公式を以下に掲げます。
さも、この年寄がジョンソンノイズの公式を覚えていたような書きぶりですが、そんなことはありません。たまたま別シリーズ「OPアンプ大全を読む」にてジョンソンノイズに向き合わざるを得なかったためです。以下の回など御覧じろ。
OPアンプ大全を読む(20) 引用「もっとも一般的に使われる係数は6.6である」、雑音尖頭値
上記公式で得られるのはRMS(二乗平均の平方根)値です。実際のノイズは「確率的な存在」なので、何時どのようなレベルのノイズが観察できるのかは不明。しかし、上記式で求めたRMS値のxx倍といったスレッショルド値を決めると、一定期間のうちノイズの尖頭値がスレッショルド値を上回っている時間割合(期待値)が計算できるっと。スレッショルドをRMS値の6.6倍にとったとき、その割合はたったの0.1%だと。
ごたごた書きました(皆、アナデバ様の『OPアンプ大全』の受け売り)ですが、そのような確率的な観察に基づく(大き目の抵抗の両端に発生する電圧をADにかけられる程度に増幅して観察し続ければ何か求まるのでないの?知らんけど)乱数発生の筈。そのため、NORDIC社のドキュメントには以下のような注意が書かれてました。一か所引用させていただきます。
The time needed to generate one random byte of data is unpredictable
“unpredictable”、いい響きです。予想できないからこそ真性な乱数の雰囲気を醸すと。
今回実験したコード
ごたくを並べた割に実験用のGoのソース、短か。machine.GetRNG()を読んでやれば32ビット符合無の結果を得ることができるからです。それだけではあんまりなので、先ほど指摘のあった、”unpredictable”な、乱数生成時間もついでに測るようにしてみました。
package main
import (
"fmt"
"machine"
"time"
)
func main() {
for {
start := time.Now()
rnd, er := machine.GetRNG()
itvl := time.Since(start).Microseconds()
if er != nil {
fmt.Printf(er.Error())
return
}
fmt.Printf("RNG : %d (%d[usec])\r\n", rnd, itvl)
time.Sleep(time.Second * 1)
}
}
実験結果
上記のコードを micro:bit v2機に書き込んで走らせた結果が以下に。生成された乱数値と、生成に掛かった時間(時刻計測のオーバヘッドも含む)が以下に。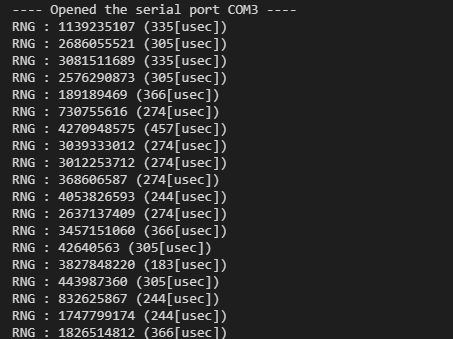
約300点ほどの数値を表計算してみたものが以下に。発生した乱数の平均値より小さい点数と、平均値以上の点数を比べてみましたが、それらしいんでないかと。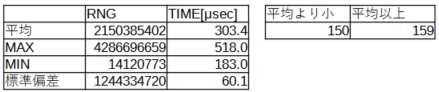
また、乱数の生成時間、確かにバラついているみたいです。でもま、上記の程度の計算(計測?)時間が許せるのであれば、「物理現象(納得?のボルツマン定数が出てくる)」に基づく乱数を使うのはありだと(個人の感想です。)ま、良いか悪いかは自分で調べてくだされや。