R言語のサンプルデータセットをABC順(大文字先)で端から試してみています。今回はお薬ネタ再びです。テオフィリン、どうも喘息などで処方される薬のようです。これの薬物動態、時間に対する血中濃度を処理するもの。何度かお薬ネタをやっているうちに、何だかよく分からないけれど処理の手順は覚えましたぜ。
※「データのお砂場」投稿順Indexはこちら
まずは、サンプル・データセットの解説ページへのリンクです。
Pharmacokinetics of Theophylline
データセットは、theophylline(日本語では「テオフィリン」でよいようです)について、12名の人(体重 kg およびドーズ量 mg/kgが異なる)の服薬から約24時間後くらいまでの時間(hr)と血中濃度(mg/L)を記録したもののようです。
お薬ネタなので深入りは避けますが、キサンチン系気管支拡張剤とて、喘息時に処方される薬みたいです。どうも副作用などもあり、血中濃度についてはいろいろ調べられてきた背景があるようです。知らんけど。
まずは生データ
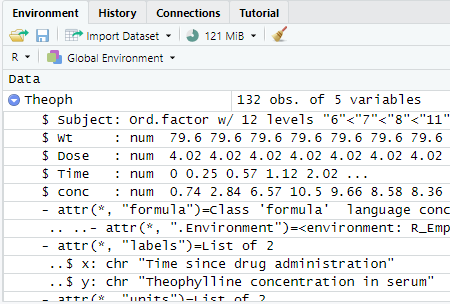
何時ものとおり、生データをロードして、形式を確かめてみます。過去なんども登場した古い形式の「修飾」のついた data.frame みたいです。コマケー話は抜きにして、単なる data.frame として扱ってよいものだと思います。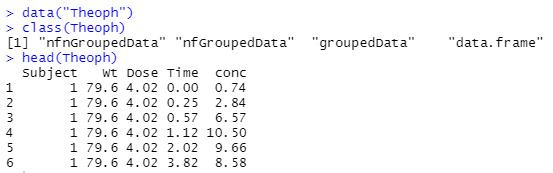
上記のhead()で生データの上の方を見てます。RStudio使っている場合は、変数の中身が右上の方のWindowでいつも見えているので以下の方が分かり易いです。Subject(患者さんの番号みたいです)は12レべル(12名様)と。
最初のグラフは自力で描くのよ
今回もサンプルデータセットの解説ページには処理例が記されています。少しでも自力で処理しないと勉強にならないので、自力でグラフを描いてみます。最初の1枚は、ggplot2を使って12名様全てのデータを1葉のグラフに描くもの。
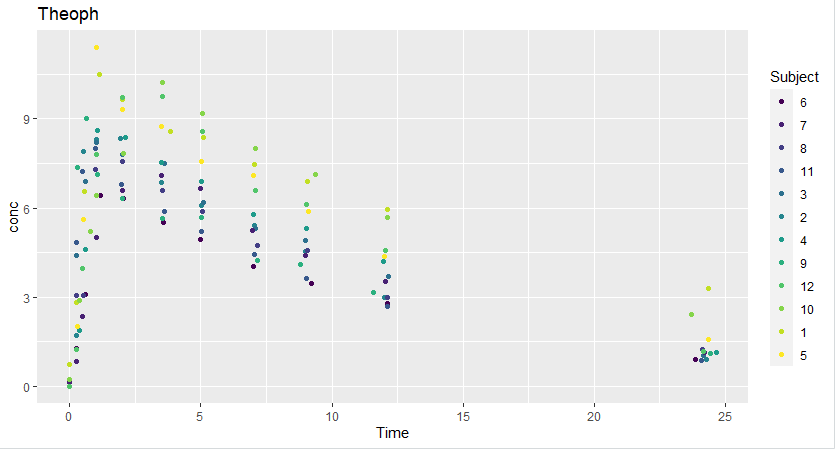
library(ggplot2) g0 <- ggplot(data=Theoph, aes(Time, conc, color=Subject))+geom_point() + labs(title="Theoph") g0
描いてみたところが以下に。
急激に上がって、ダラダラ落ちますが、基本イクスポーネンシャル・カーブっすかね。ざっくりした印象(電子系のアナロジー)でいうと、「立ち上がりと立ち下りの時定数が異なる」波形に見えます。
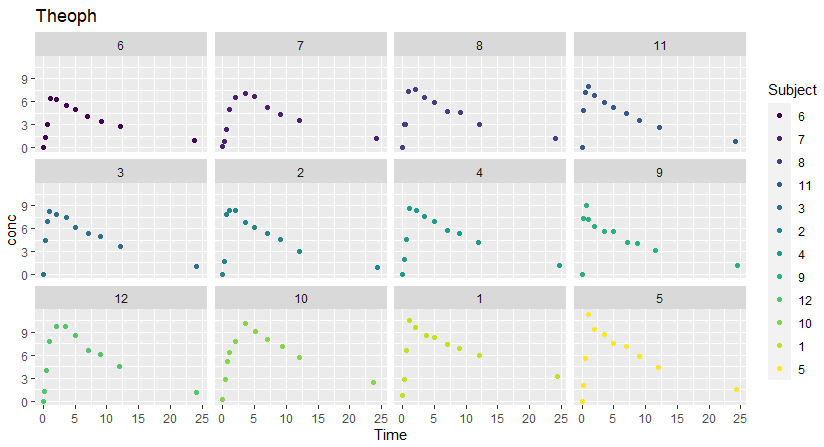
つづいて、患者さん毎にファセットを切ってグラフを分けてみます。こういう追加が出来るのがggplot2の良いところ。
g1 <- g0 + facet_wrap(vars(Subject)) g1
ファセット切ったグラフが以下に。例によって成り行きで色を振っているので、黄色が見難いくてすみません。
自力更生はここまで。ほんとちょっとだけだな、自分。
処理例をなぞる
ここからは解説ページをなぞっていきたいと思います。上記のグラフを見れば分かる通り、この先は
-
- 非線形のモデルをもってきてフィットさせる
- それに基づいて回帰曲線を引く
というステップがある筈。しかし、そのフィットさせるモデルにどんなものがあるのか私は知らないっと。
処理例でも最初は患者さん毎のグラフを描いてます。こちらは coplot()利用。
グラフは以下のようです。色味が薄い分、アカデミックな感じがする?ホントか。気のせいだし。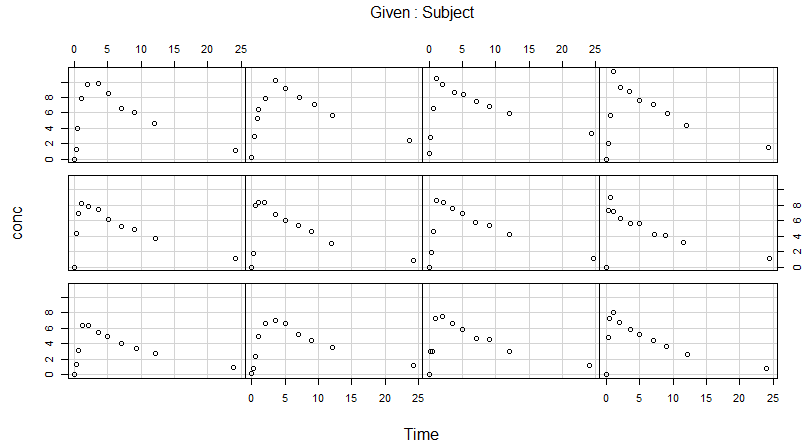
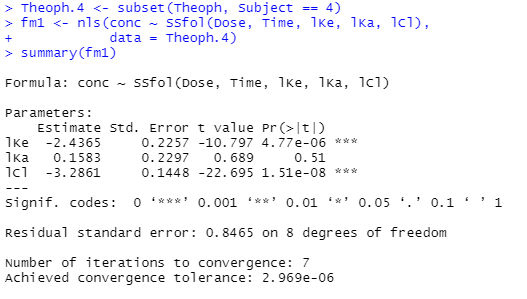
さて、つづいて12名さまから、Subject番号4番の人のデータだけを取り出して処理することにしたようです。なんで4番なのかは分かりませんが、どうせ全部処理するうちの最初の例ということなんでしょ。
例によって非線形のために nls() を読んでフィットさせています。そこで登場するモデルの御名前が ssfol とな。
フィットさせた結果は上記にありますが、肝心の SSfol モデルについては不明。SSfolモデルの説明ページは以下にありました。
Self-Starting Nls First-order Compartment Model
ファースト・オーダー・コンパートメント・モデルとな。これだけ聞いても何やらサッパリなのですが、ググれば道は開けると。以下のページを参照させていただきました。
どうも、コンパートメントモデルというのは薬物動態学では基本的なモデルみたいです。ついつい電子系的な世界へのアナロジーを書かせていただくと
ブロックダイアグラム
に似ている感じ。各要素に入力があり出力があり、それを接続していって全体モデルができると。そして SSfol モデルというのはその中でもRC回路的な簡単なモデルの伝達関数みたいなもの?という印象をうけました。SSfolと言われるとビビりますが、伝達関数ならOKっと(ホントか?伝達関数の計算もヤバそうだが、自分)
上記で4番目の患者さんにフィットした係数が求まっているので、非線形の回帰曲線を描くことができると、処理例によればこんな感じ。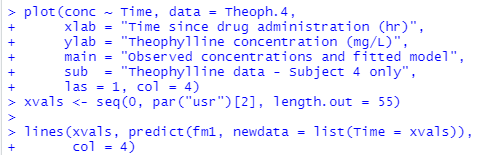
例によって分かったような、分からぬようなな結果でありますが、手を動かして処理する定石には慣れたような気がします。錯覚だぜ、もしかすると。