前回、スマホ上のGo言語を使ってマンデルブロ集合を描いてみました。この時作ったGo言語のソースは昔作ったExcelのVBAソースを移植したものです。忘れていたのですが、PCにもスマホにもそこかしこにマンデルブロ集合が隠れてました。今回はその幾つかを「呼び出して」みます。
※「やっつけな日常」投稿順 indexはこちら
Webで検索すればマンデルブロ集合を定義する非常に簡単な漸化式が見つかると思います。この集合を複素平面(実際には虚数軸をY軸として2次元平面)にプロットすれば良いっと。黒く抜けている部分こそマンデルブロ集合であって、その他の色は集合からの近さを見栄えよく示しておるっと。
なんだか瓢箪的な図形が見えてきますが、その一部、集合の境界部分を拡大するとまた似たような瓢箪が現れ、その先を拡大するとまた、という具合になっているフラクタルの「代表選手」といって良いのじゃないかと覆います。
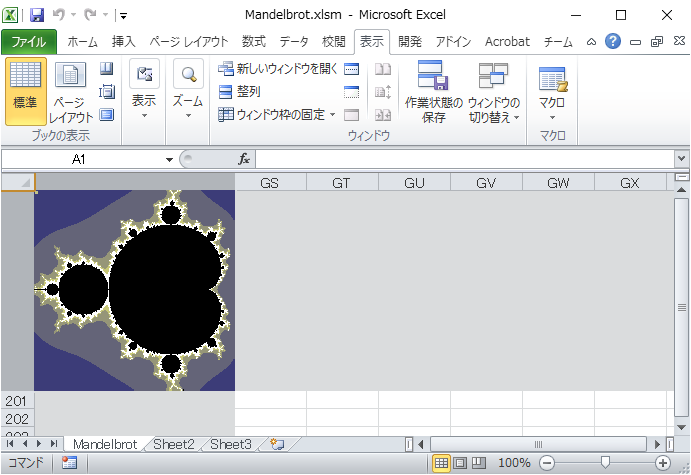
Excel版のマンデルブロ集合描画
以下のコードは前提がいくつかあります
-
- VBAを走らせることができて、以下のコードがVBAスクリプトとしてワークシート内に記録されていること
- mandelbrotと名付けたシートがある(出力で書き換えてしまう)
- VBAのサブルーチン GoMandel() を実行する
古い既にメンテナンスも切れているExcel2010で動作確認してます。最近のExcelは、VBAのような危険なものを走らせることに対してセキュリティ上の観点から制限かかっているような気がするので、VBAの許可手順があるんじゃないかと思います。
前回Goに移植済の古いVBAのコードが以下に
Sub GoMandel()
Dim i As Integer
Dim j As Integer
Dim pa As Double
Dim pb As Double
Dim mdlev As Integer
With Worksheets("mandelbrot")
.Activate
.Range(Cells(1, 1), Cells(200, 200)).RowHeight = 1
.Range(Cells(1, 1), Cells(200, 200)).ColumnWidth = 0.1
For i = 1 To 200
pa = -1.5 + CDbl(i) / 100
For j = 1 To 200
pb = 1# - CDbl(j) / 100
mdlev = mandelbrot(pa, pb)
Select Case mdlev
Case Is > 999
Cells(j, i).Interior.Color = RGB(0, 0, 0)
Case Is > 20
Cells(j, i).Interior.Color = RGB(255, 255, 255)
Case Is > 15
Cells(j, i).Interior.Color = RGB(200, 200, 120)
Case Is > 10
Cells(j, i).Interior.Color = RGB(150, 150, 120)
Case Is > 5
Cells(j, i).Interior.Color = RGB(100, 100, 120)
Case Is > 3
Cells(j, i).Interior.Color = RGB(60, 60, 120)
Case Is > 2
Cells(j, i).Interior.Color = RGB(20, 20, 120)
Case Else
Cells(j, i).Interior.Color = RGB(10, 10, 80)
End Select
Next
Next
End With
End Sub
Function mandelbrot(ByVal a As Double, ByVal b As Double) As Integer
Dim x As Double
Dim y As Double
Dim xn As Double
Dim yn As Double
Dim r As Double
Dim cnt As Integer
x = 0#
y = 0#
cnt = 0
r = 0#
Do
xn = x ^ 2 - y ^ 2 + a
yn = 2# * x * y + b
r = xn ^ 2 + yn ^ 2
x = xn
y = yn
cnt = cnt + 1
Loop Until (cnt > 999) Or (r > 100#)
mandelbrot = cnt
End Function
上記のコードを実行すると Mandelbrotと名付けたシート上にマンデルブロ集合が現れますです。こんな感じ。
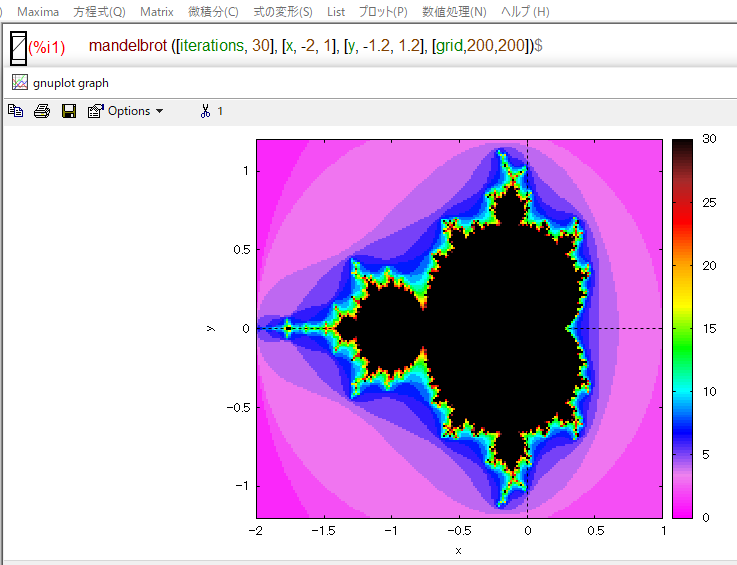
Maxima上でマンデルブロ集合
最近、別シリーズでお世話になっておりますMaxima様には、そのものズバリのmandelbrot()関数が含まれています。それに引き数を与えて動かせば、gnuplotが開いてマンデルブロ集合を描いてくれます。こちらの方が「光背」が華やかな色合い。集合そのものは黒1色で変わりませぬが。
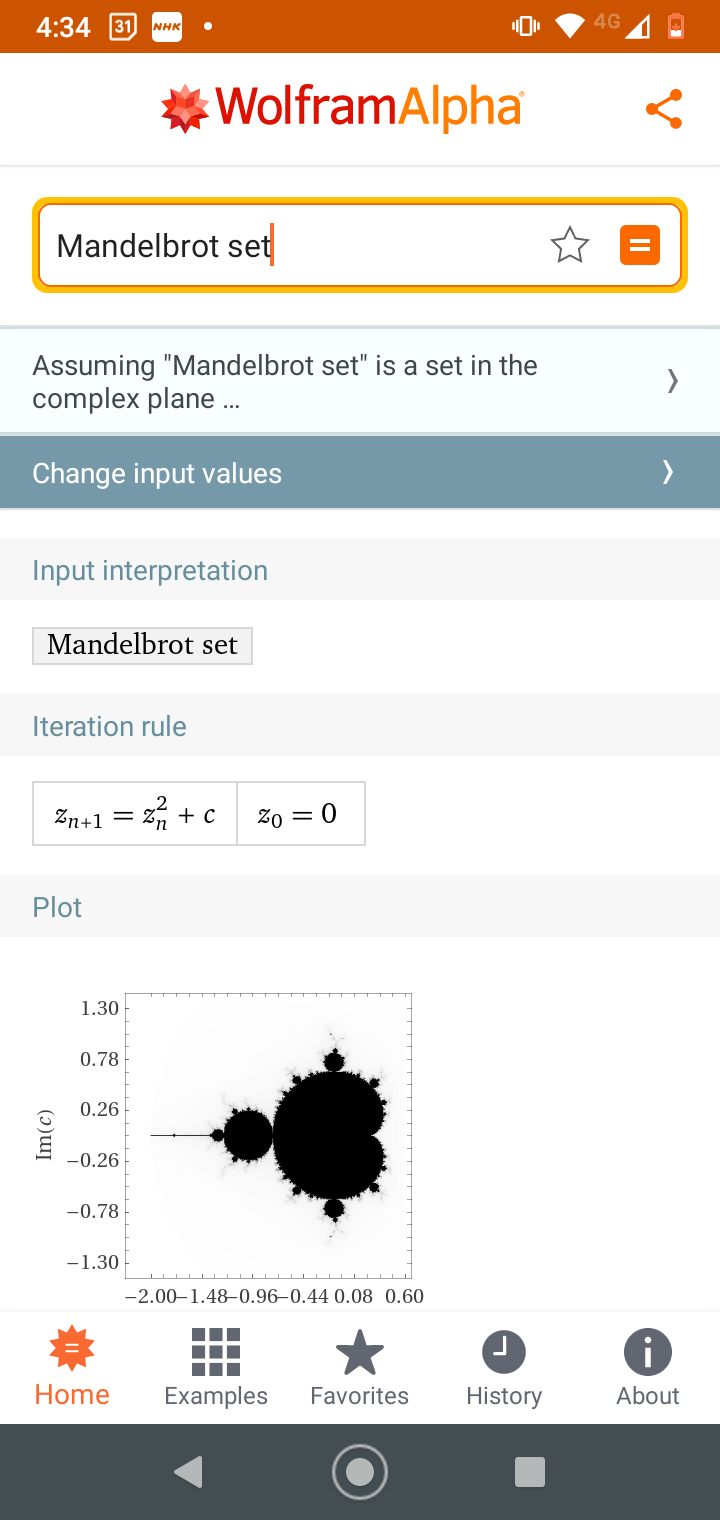
WolframAlphaでマンデルブロ集合
Androidスマホ上では、わざわざプログラムをGo言語で書き直さなくても、実はマンデルブロ集合が見られることに気づきました。MathematicaでおなじみのWolfram社のアプリ
を数年前にインストール(有料)してあったからです。上のリンクから辿れるWebバージョンは無料だし、日本語充実しているし。。。
スマホアプリ版は、上手く使おうとすると英語力が必要なアプリだと思います(それで買った割に稼働率低。)今回も最初
mandelbrot
と入力したら、発見者のMandelbrot様が登場してしまいました。長生きだったのね。
Mandelbrot set
ちゃんと漸化式も書いてあるし(当たり前か。)スクロールダウンしていくと、プロットの一部を拡大できるウインドウがあり、そこで場所を選びながらズームして「フラクタル」を味わうことができるようになっとります。流石だなWolframAlpha。
これ以外にもマンデルブロ集合、アチコチに潜んでおるような気がします。