前回は正弦波を計算で生成するためにミニマックス近似を使ったFastSin関数を使わせていただきました。12ビットの精度なら十分使えて「速い」と三上先生の御本にはあるのです。しかしどのくらい速いのだか気になります。今回は実機(Arm Cortex-M4F)上でどのくらい速いのだか測定してみたいと思います。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※今回はいつもと違って実習には Nucleo-F401REボード(ST Microelectronics社製。搭載CPUは Arm Cortex-M4F でF446REと同じ)を使っております。また、ビルドにはArm社のWeb開発環境 Mbed Webコンパイラを利用させていただいておりますが、「手習ひデジタル信号処理」でいつも使わせていただいとりますOS2ではなく、OS6を使用しております。別シリーズ「モダンOSのお砂場」で使っている道具だてであります。
※参照させていただいております三上直樹先生著の教科書は以下です。
工学社『「Armマイコン」プログラムで学ぶデジタル信号処理』
三上先生の御ソースはArm社のMbed環境(要登録、無料)で公開されており、「呂」で検索すれば発見できます。
実行サイクル数を測定
「表」のカウンタ類は「仕事」に使う可能性があるので、性能測定には純然たるそれ用のカウンタがあるものです。Arm Cortex-M4Fにもパフォーマンス・カウンタ(サイクル・カウンタ)があったよなあ、ということで調べてみました。この辺は多分実装依存(メーカの考え方による)なので、半導体メーカによって実装レベルは異なるはず。STM32マイコンのメーカであるST Microelectronics社の日本語解説ページをみると以下2件の記述を発見しました。
「使える」(ST社が実装している)ということは上記ページでほぼ確認とれたのですが、どう使ったら良いのかは上記説明からはイマイチ釈然とせず。Arm社公式の以下に関係レジスタが列挙されておりますのでそちらを見ます。
まずは、使えることを以下のレジスタを読み取って実機確認してみました。
DWT_CTRLレジスタ (0xE0001000)
読み出した初期値は 0x40000000 でした。上記のArm公式から1行引用させていただきましょう。
four comparators for watchpoints and triggers are present.
さすがST社です。ケチらずちゃんと実装してくれているみたいです。なお、上記DWTのサイクルカウンタを使うためには、DWTに活を入れて(クロック与えて動かして)おかないとならんみたいでした。そこについては以下に。
Debug Exception and Monitor Control Register
上記レジスタのビット24のTRCENAビットをONにするとDWTだけでなく、以下の奴らが(存在していれば)皆動き始めるみたいです。なお、デフォルトはOFFです。
-
- Data Watchpoint and Trace (DWT)
- Instrumentation Trace Macrocell (ITM)
- Embedded Trace Macrocell (ETM)
- Trace Port Interface Unit (TPIU)
実験用ソース
三上先生のFastSin() 関数はインライン関数として定義されているので、ヘッダを取り込んで使用させていただきました。ミニマックス近似は単なる浮動小数の多項式の計算なので、OS2だろうがOS6だろうが共用可能でした。
mathヘッダで呼び出せる標準関数 sin() 単精度と、三上先生御ソースのFastSin() をほぼ同じ引数に対して呼び出して実行にかかったサイクル数を測定してみました。ほぼというのは、sin()関数は定義がラジアンですが、FastSin()は π/2 ラジアンが1となるような単位系?で定義されているので、サイクル数の測定にかからない部分で単位を合わせて見やすくしているためです。また、math.h の中に M_PI定数入ってなかったので、勝手に単精度の円周率を定義しました。
なおsin()関数は「関数」でコール、リターンのオーバヘッドが含まれる筈ですが、FastSin()はインライン展開されるのでその分のオーバヘッドもありません。有利といっても数サイクル単位だと思いますが。
いつもの冗長なソースが以下に。
#include "mbed.h"
#include "platform/mbed_thread.h"
#include "stdlib.h"
#include "math.h"
#include "FastSin.hpp"
using namespace Mikami;
#define MY_PI (3.141693f)
//DWT_REGISTERS
int *DWT_CTRL = (int *)0xE0001000;
int *DWT_CYCCNT = (int *)0xE0001004;
int *DEMCR = (int *)0xE000EDFC;
int saveDWT_CTRL;
void measureSin(float x)
{
int endCYC;
float y;
x *= MY_PI/2.0f;
*DWT_CYCCNT = 0;
*DWT_CTRL = saveDWT_CTRL | 1;
y = sin(x);
endCYC = *DWT_CYCCNT;
*DWT_CTRL = saveDWT_CTRL;
printf(" sin(%f)=%f CYC:%d\r\n", x, y, endCYC);
}
void measureFastSin(float x)
{
int endCYC;
float y;
*DWT_CYCCNT = 0;
*DWT_CTRL = saveDWT_CTRL | 1;
y = FastSin(x);
endCYC = *DWT_CYCCNT;
*DWT_CTRL = saveDWT_CTRL;
printf("FastSin(%f)=%f CYC:%d\r\n", x*(MY_PI/2.0f), y, endCYC);
}
int main()
{
float x, stp;
saveDWT_CTRL = *DWT_CTRL;
*DEMCR |= (1UL << 24);
printf("\r\n DWT_CTRL: %08x\r\n", *DWT_CTRL);
x = 0.0f;
stp = 1/9.0f;
while (true) {
if (x > 1.0f) x = 0.0f;
measureSin(x);
measureFastSin(x);
x += stp;
thread_sleep_for(5000);
}
}
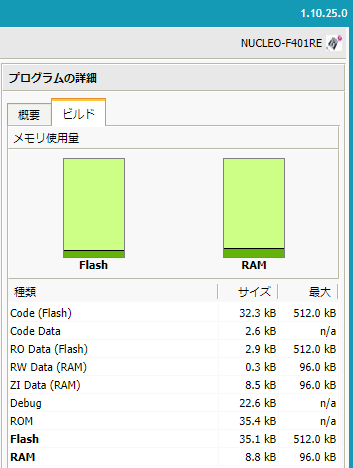
ビルド結果
今回は単精度とはいえ浮動小数のsin()なのでどのくらいのメモリが必要になるのだかちょっと心配だったです。しかしまったく問題なし。「いつもの」F446REであれば今回使用のF401REよりもフラッシュは多いので余裕の筈。
実行結果
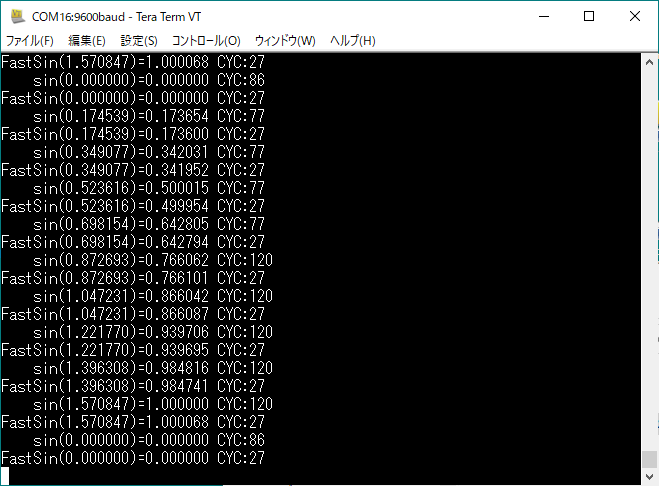
実機のUSBシリアルにTeratermを接続して結果を観察したところが冒頭のアイキャッチ画像に。実際のサイクル数は読み値-2で良さそうなので、実行サイクル数の比較結果が以下に
-
- 標準sin() 関数、引数により最短75サイクル、最長118サイクルと変化
- FastSin() 関数、引数による変動なし、25サイクル
標準のsin()関数は、どうも π/4 を超えるか超えないかで処理パスが異なる感じがします。また、引数0のときも違うみたい。それに対してFastSin()関数は速いです。3~5倍も速い感じ。小数点以下3桁目までは結果あっているし、4桁目も近い値だし。浮動小数(単精度)で計算をアクセラレートするときはミニマックス近似だね(固定小数点ならCORDIC、多分。知らんけど。)