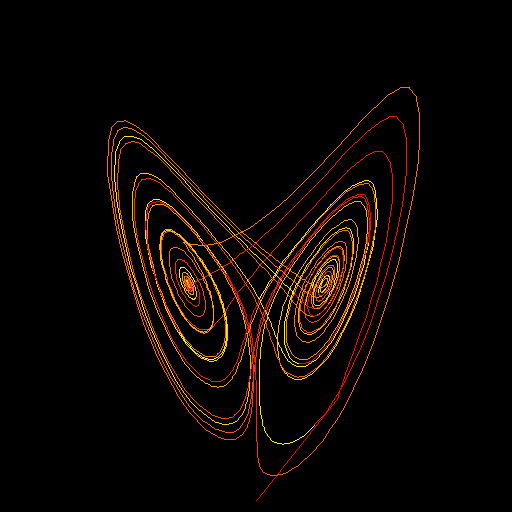やっつけな日常(13) スマホでGo！じゃない。全てを引きこむローレンツアトラクタ

スマホの上でGo言語を学んでいる筈が、だんだんカオスとかフラクタルな図形と戯れるシリーズになってしまっております。今回は完全に羊頭狗肉、Goを走らせているのはWSL1上のUbuntu 20.04LTS環境です。どうせスマホの上でも無変更で実行可能だから良いのだ、と言い訳。

※「やっつけな日常」投稿順 indexはこちら

※内部で使用しているローカル・モジュールのコード全文（改訂版）は末尾にまとめて掲載しました。

なにやら不気味な「ストレンジ・アトラクタ」の代表選手が「ローレンツ・アトラクタ」であります。初期値に何を与えても、ストレンジなアトラクタに引き込まれてしまうっと。ローレンツアトラクタとかローレンツ方程式とかで検索すれば多数ヒットすると思います。

今回実験のソース

ローレンツ方程式（非線形常微分方程式、３次元空間内に軌跡を描く）はコードとしてはとても簡単、下のメイン関数の中のfor文の中の６行ばかりの計算がそれです。他は、初期値を設定したり、色を変えたりのデコレーションです。

X、Y、Zの３次元空間なのですが、描いているのはY軸に平行な視点からX軸（横）、Z軸（縦）を眺めたところです。視点の移動は含まれていません。

今回は初期値をいろいろ変更しても、アトラクタに引き込まれるところを見たかったので、コマンドラインパラメータはやや充実？してます。

Go言語のお勉強部分は大した進捗もなく、以下の１点くらいです。

画像のファイル出力関数を追加した。ファイル名はコマンドラインオプションで与えるようにした。

参照させていただいたのは以下のページです。

Go by Example: Writing Files

また、大した追加でもないのですが、自作のPPM出力、タートルグラフィクスのライブラリモジュールにまた手を入れてしまったです。全文を末尾に掲げました。

• • 途中経過を標準エラーに出力する機能をフラグでON/OFFできるようにした。
  • タートルグラフィクスモジュール内に座標を指定して線を描ける、全然タートルでない関数を追加した。

メイン関数 Lorenz.go のソースが以下に。

package main

import (
  "flag"
  "local/turtle"
  "local/ppm"
)

func main() {
  fnam    := flag.String("f", "Lorenz_default.ppm", "PPM file name")
  xPtr := flag.Float64("x", 1.0, "Initial value X, float64")
  yPtr := flag.Float64("y", 1.0, "Initial value Y, float64")
  zPtr := flag.Float64("z", 1.0, "Initial value Z, float64")
  itrPtr := flag.Int("itr", 3000, "Iteration count, Int")
  stpPtr := flag.Float64("stp", 0.01, "Step parameter, float64")
  verbose := flag.Bool("v", false, "verbose flag")
  flag.Parse()
  var img ppm.PpmImage
  XMAX:= 512
  YMAX:= 512
  img.InitPpmImage(XMAX, YMAX, 256)
  img.Verbose = *verbose
  var ttl turtle.TurtleGraphics
  ttl.InitTurtleGraphics(256, 500, 8.0, img.Line)
  x := *xPtr
  y := *yPtr
  z := *zPtr
  p := 10.0
  r := 28.0
  b := 8.0 / 3.0
  var dx, dy, dz float64
  for i:=0; i < *itrPtr; i++ {
    dx = p * (y - x)
    dy = x * (r - z) - y
    dz = x * y - b * z
    x += *stpPtr * dx
    y += *stpPtr * dy
    z += *stpPtr * dz
    g := i % 256
    b := i / 256
    ttl.Color(255, g, b)
    ttl.Draw(x, z)
  }
  img.FwritePPM(*fnam)
}

実行結果

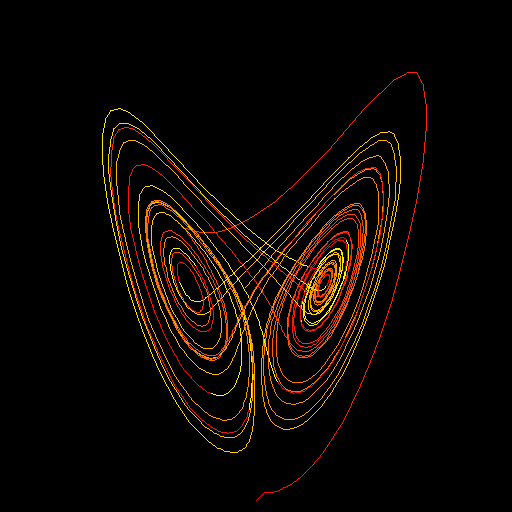
冒頭のアイキャッチ画像に掲げましたのが以下の初期値のケースです。

• • x = 1.0
  • y = 1.0
  • z = 1.0

デフォルト値なので

$ go run Lorenz.go -f Lorenz_1_1_1.ppm
$ convert Lorenz_1_1_1.ppm Lorenz_1_1_1.png

でPNG画像を得ることができます。

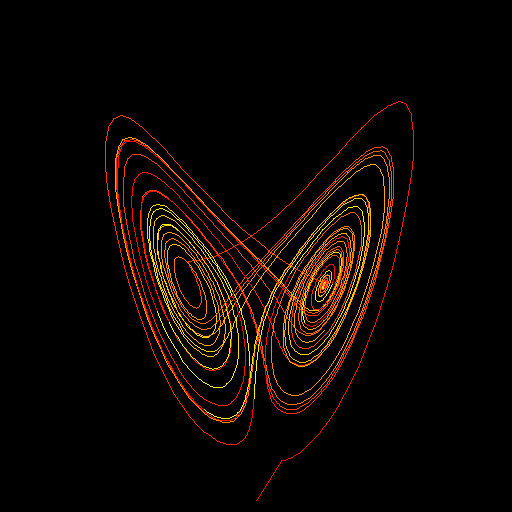
以下の画像の初期値は以下です。

• • x =3.0
  • y = 4.0
  • z = 5.0

$ go run Lorenz.go -x 3.0 -y 4.0 -z 5.0 -f Lorenz_3_4_5.ppm
$ convert Lorenz_3_4_5.ppm Lorenz_3_4_5.png

でPNG画像を得ることができます。

以下の画像の初期値は以下です。

• • x =10.0
  • y = 11.0
  • z = 12.0

$ go run Lorenz.go -x 10.0 -y 11.0 -z 12.0 -f Lorenz_10_11_12.ppm
$ convert Lorenz_10_11_12.ppm Lorenz_10_11_12.png

でPNG画像を得ることができます。

並べてみると、初期値により微妙に軌道が異なるのが分かるのですが、どれも変わり映えがしません。ストレンジといいつつ、沢山描くと退屈な。ホントか？

やっつけな日常(12) スマホでGo！1.26186…次元から染み出すコッホ曲線　へ戻る

やっつけな日常(14) スマホでGo！パラメータを変えると飽きない２分木？を描く。へ進む

ppm.go

package ppm
import (
  "bufio"
  "fmt"
  "os"
)

type PpmImage struct {
  width int
  height int
  cmax int
  buf []int
  Verbose bool
}

func (this *PpmImage) InitPpmImage(w int, h int, cx int) bool {
  this.width = w
  this.height = h
  this.cmax = cx
  this.buf = make([]int, w*h*3)
  this.Verbose = false
  return true
}

func (this *PpmImage) DotXY(x int, y int, r int, g int, b int) bool {
  if (x < 0) || (x >= this.width) || (y < 0) || (y >= this.height) {
    return false
  } else {
    this.buf[3*(y*this.width + x)]     = r
    this.buf[3*(y*this.width + x) + 1] = g
    this.buf[3*(y*this.width + x) + 2] = b
  }
  return true
}

func (this *PpmImage) WritePPM() bool {
  fmt.Println("P3")
  fmt.Println(this.width, " ", this.height)
  fmt.Println(this.cmax)
  for y := 0; y < this.height; y++ {
    for x := 0; x < this.width; x++ {
      fmt.Print(  this.buf[3*(y*this.width + x)], " ")
      fmt.Print(  this.buf[3*(y*this.width + x) + 1], " ")
      fmt.Println(this.buf[3*(y*this.width + x) + 2])
    }
  }
  return true
}

func (this *PpmImage) FwritePPM(fnam string) bool {
  f, err := os.Create(fnam)
  if err != nil {
    return false
  }
  defer f.Close()
  w := bufio.NewWriter(f)
  fmt.Fprintf(w, "P3\n")
  fmt.Fprintf(w, "%d %d\n",this.width, this.height)
  fmt.Fprintf(w, "%d\n", this.cmax)
  for y := 0; y < this.height; y++ {
    for x := 0; x < this.width; x++ {
      fmt.Fprintf(w, "%d ", this.buf[3*(y*this.width + x)])
      fmt.Fprintf(w, "%d ", this.buf[3*(y*this.width + x) + 1])
      fmt.Fprintf(w, "%d\n",this.buf[3*(y*this.width + x) + 2])
    }
  }
  w.Flush()
  return true
}

grad2d.go

package ppm

import (
  "fmt"
  "os"
)

func (this *PpmImage) Box(x1 int, y1 int, x2 int, y2 int, r int, g int, b int) bool {
  if x1 > x2 {
    x1, x2 = x2, x1
  }
  if y1 > y2 {
    y1, y2 = y2, y1
  }
  for x := x1; x<=x2; x++ {
    this.DotXY(x, y1, r, g, b)
    this.DotXY(x, y2, r, g, b)
  }
  for y := y1; y<=y2; y++ {
    this.DotXY(x1, y, r, g, b)
    this.DotXY(x2, y, r, g, b)
  }
  return true
}

func (this *PpmImage) Line(x1 int, y1 int, x2 int, y2 int, r int, g int, b int) bool {
  var dx int
  var dy int
  var x, y int
  var revx bool = false
  var revy bool = false
  if x1 > x2 {
    dx = x1 - x2
    revx = true
  } else {
    dx = x2 - x1
  }
  if y1 > y2 {
    dy = y1 - y2
    revy = true
  } else {
    dy = y2 - y1
  }
  if dx > dy {
    if this.Verbose {fmt.Fprintln(os.Stderr, "X mode ", x1, y2, dx, dy)}
    if revx {
      if this.Verbose {fmt.Fprintln(os.Stderr, "REVX")}
      x1, x2 = x2, x1
      y1, y2 = y2, y1
    }
    dy = y2 - y1
    for x= 0; x<=dx; x++ {
      if dx != 0 {
        y= (dy * x) / dx
      } else {
        y= 0
      }
      this.DotXY(x+x1, y+y1, r, g, b)
    }
  } else {
    if this.Verbose {fmt.Fprintln(os.Stderr, "Y mode", x1, y2, dx, dy)}
    if revy {
      if this.Verbose {fmt.Fprintln(os.Stderr, "REVY")}
      x1, x2 = x2, x1
      y1, y2 = y2, y1
    }
    dx = x2 - x1
    for y= 0; y<=dy; y++ {
      if dy != 0 {
        x= (dx * y) / dy
      } else {
        x= 0
      }
      this.DotXY(x+x1, y+y1, r, g, b)
    }
  }
  return true
}

turtle.go

package turtle

import "math"

type LineFunc func(x1 int, y1 int, x2 int, y2 int, r int, g int, b int) bool

type TurtleGraphics struct {
  xpos float64
  ypos float64
  direction float64
  ijSCALE float64
  iORG int
  jORG int
  ipos int
  jpos int
  iold int
  jold int
  colR int
  colG int
  colB int
  penDOWN bool
  line LineFunc
  verbose bool
}

func (t *TurtleGraphics) InitTurtleGraphics(x int, y int, sca float64, lf LineFunc) bool {
  t.xpos = 0.0
  t.ypos = 0.0
  t.direction = 0.0
  t.colR = 128
  t.colG = 128
  t.colB = 128
  t.penDOWN = true
  t.verbose = false
  t.line = lf
  t.ijSCALE = sca
  t.iORG = x
  t.jORG = y
  t.ipos = x
  t.jpos = y
  return true
}

func(t *TurtleGraphics) Mov(dist float64) bool {
  t.xpos += math.Cos(t.direction)*dist
  t.ypos += math.Sin(t.direction)*dist
  t.iold = t.ipos
  t.jold = t.jpos
  t.ipos = int(math.Round(t.xpos * t.ijSCALE)) + t.iORG
  t.jpos = t.jORG - int(math.Round(t.ypos * t.ijSCALE))
  if t.penDOWN {
    t.line(t.iold, t.jold, t.ipos, t.jpos, t.colR, t.colG, t.colB)
  }
  return true
}

func(t *TurtleGraphics) Rot(theta float64) bool {
  rad := theta * math.Pi / 180
  t.direction += rad
  if t.direction < (-math.Pi) {
    t.direction = 2.0*math.Pi + t.direction
  } else if t.direction > math.Pi {
    t.direction = t.direction - 2.0*math.Pi
  }
  return true
}

func(t* TurtleGraphics) Color(r int, g int, b int) {
  t.colR = r
  t.colG = g
  t.colB = b
}

func(t* TurtleGraphics) PenDown(x bool) {
  t.penDOWN = x
}

func(t *TurtleGraphics) Draw(x float64, y float64) bool {
  t.xpos = x
  t.ypos = y
  t.iold = t.ipos
  t.jold = t.jpos
  t.ipos = int(math.Round(t.xpos * t.ijSCALE)) + t.iORG
  t.jpos = t.jORG - int(math.Round(t.ypos * t.ijSCALE))
  if t.penDOWN {
    t.line(t.iold, t.jold, t.ipos, t.jpos, t.colR, t.colG, t.colB)
  }
  return true
}